|
ГЛАВА 8
АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ
Ответы и решения
825. Пусть в 1 мин. большее колесо делает х оборотов, а меньшее у оборотов, у > х. Имеем уравнения
у — х = 400; 5/x — 5/у = 1/60
Второе уравнение можно представить в виде xy = 300(y—х), т. е, xy =120 000.
Отв. Большее колесо делает 200 оборотов в минуту, меньшее - 600 оборотов.
__________________________________________________
826. Пусть окружность переднего колеса равна х дм, а окружность заднего - у дм. Имеем два уравнения:
180/x — 180/у = 10
и
180/x+6 — 180/у—6 = 4
Первое преобразуется к виду 18 (у — х) = xy ; второе — к виду 39(у — х) = xy + 504. Из этих двух уравнений найдем у — х = 24; xy = 432.
Отв. Окружность переднего колеса 12 дм, заднего - 36 дм.
__________________________________________________
827. В первый и третий дни было выгружено 600 • 2/3 = 400 т; во второй день выгружено 600 т—400 т = 200 т. Пусть в первый день выгружено х т; тогда в третий день выгружено (400—х) т. Уменьшение выгрузки во второй день по сравнению с первым днем было (х—200) т, что составляло 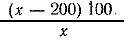 % от выгрузки первого дня. % от выгрузки первого дня.
Уменьшение выгрузки в третий день по сравнению со вторым днем было
200—(400—х) = (х—200) т. что составляло
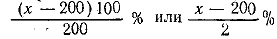 % выгрузки второго дня. По условию % выгрузки второго дня. По условию
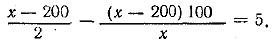
Найдем два корня x1= 250; x2=160. Второй корень не годится , так как по условию выгрузка с каждым днем уменьшалась, между тем как при х=160 выгрузка составляла бы: в первый день 160 т, во второй 200 т и в третий 240 т.
Отв. В первый день было выгружено 250 т, во второй 200 т, в третий 150 т.
__________________________________________________
828. Пусь первый раствор весит х кг, тогда второй весит (10—х) кг. Процентное содержание безводной серкой кислоты в первом растворе 
По условию 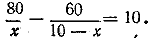
Уравнение имеет два положительных корня x1 = 20 и x2= 4. Так как по условию x < 10, тo первое решение не годится.
Отв. 4 кг и 6 кг.
__________________________________________________
829. Если в первом сплаве было х% меди, то во втором было (х+40)%. Первый сплав весил 6*100/х кг, а второй 12*100/х кг. Получаем уравнение
600/x + 600/x+40 = 50.
Отв. 20% и 60%.
__________________________________________________
830. Пусть скорость товарного поезда x м/сек, а пассажирского у м/сек. За 28 сек. товарный поезд прошел 28 х (м), а пассажирский 28 у (м); получаем уравнение
28х+28у = 700.
Товарный поезд идет мимо светофора 490/x сек., а пассажирский 210/xсек. Получаем второе уравнение
490/x — 210/x = 35
Отв. Скорость товарного поезда 10 м/сек, т. е. 36 км/час, пассажирского— 15 м/сек, т. е. 54 км/час.
__________________________________________________
831. Если число четырехосных цистерн равно х, то число двухосных равно (х+5). Если одна двухосная цистерна весит у т, то одна четырехосная весит 3y т. Вес нефти в двухосной цистерне равен (40•0,3) т =12 т. Четырехосная цистерна с нефтью весит (3у+40) т, а двухосная (у + 12) т. Имеем первое уравнение
х(3y+40) + (х+5) (y +12) =940.
Вес нефти во всех четырехосных цистернах (40х), т, а вес всех груженых (х+5) (у+12) т. Имеем второе уравнение
40х— (х+5) (у+12) = 100.
Отв. Четырехосных цистерн было 10, весом каждая по 24 т., двухосных цистерн было 15, весом каждая по 8 т.
__________________________________________________
832. Пусть первая машина проходит в день х м, а вторая у м. В первом случае первая машина выполнила бы 30% всей работы, т. е. прошла бы 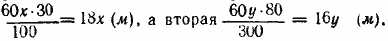
Имеем уравнение
18х+16у = 60.
Во втором случае первая машина прошла бы 22/3 • 60у (м), затратив на это 2/3 • 60• y/x дней. Вторая машина затратила бы 3/10 • 60• х/у дней.
Имеем второе уравнение
40y/x — 18х/у = 6
Полученная система легко решается, если положить y/x= z. К задаче подходит положительное значение z = 3/4
Отв. Первая машина проходит в день 2 м тоннеля;
вторая » » » » 11/2 м » .
__________________________________________________
833. Пусть первая бригада может отремонтировать участок пути в x дней, а вторая — в у дней. По условию задачи имеем систему уравнений
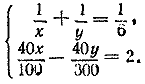
Отв. Первая бригада может отремонтировать участок в 10 дней, вторая — в 15 дней.
__________________________________________________
834. Пусть первая часть груза (составляющая 25/46• 690=375 т) была перевезена за х час, и каждая трехтонная машина делала у поездок в час. Тогда каждая полуторатонная машина делала (у+1) поездку в час. По условию вторая часть груза (т. е. 690—375= 315 т) была перевезена за (х—2) часа, причем трехтонные машины делали по (у+1) поездок в час, а полуторатонные — по (у+1)+1= (у+2) поездок. Получаем систему уравнений
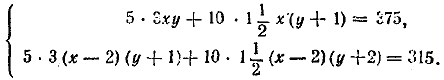
После упрощений эти уравнения примут вид
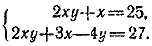
Вычитая первое уравнение из второго, получим 2х—4у=2. Отсюда 2у = х—1. Подставляя в первое уравнение, получим х2=25, т. е. х = 5. Первая часть груза была перевезена за 5 час. вторая — за 5—2 = 3 часа.
Отв. Груз перевезен за 8 час, трехтонные машины вначале делали по 2 поездки в час; потуторатонные— по 3 поездки в час.
__________________________________________________
835. Если х — ширина дорожки, то площадка вместе с дорожкой содержит
(а+2х) (b+2х) м2. Имеем уравнение (а+2х) (b+2х) = 2ab,
Отв. 1/4 [ √(a+ b)2 +4ab — (a + b)]
__________________________________________________
836. Число стульев в каждом ряду обозначим через х; тогда число рядов равно a/x Получаем уравнение
(a + b)( a/x — с ) = 1,1а.
После упрощений имеем:
10сх2+(а+10bс)х— 10аb =0.
Отсюда
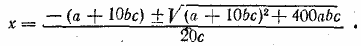
Если радикал взять со знаком минус, то х<0; если взять со знач ком плюс, то х>0.
Отв. Число стульев в каждом ряду
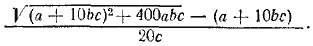
__________________________________________________
837. Обозначим скорости тел (в м/сек) через v1 и v2; пусть v1 > v2. Первое условие дает уравнение av1 + av2 = d; второе дает уравнение bv1—bv2 = d.
Отв. v1 = d/2( 1/a+ 1/b ) ; v2 = d/2( 1/a— 1/b ) Задача имеет решение только при а < b.
__________________________________________________
838. Обозначим скорость мотоциклиста (в км/час) через х, а велосипедиста — через у. Получаем систему уравнений
2х+ 2y = d; d/y— d/x = t.
Отв. Скорость мотоциклиста 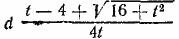 км/час, км/час,
скорость велосипедиста 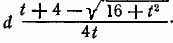
__________________________________________________
839. Если велосипедисту требуется х час, то пешеходу требуется (х+с) час. Обозначим через у расстояние АВ (скажем, в километрах). До места встречи пешеход прошел 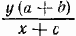 км а велосипедист проехал км а велосипедист проехал 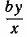 км. км.
Имеем уравнение 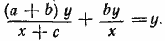
Так как у=/=0, то 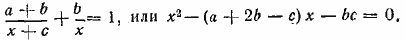
Это уравнение имеет один положительный и один отрицательный корень (так как произведение корней равно отрицательному числу —bc). Годится только положительное решение
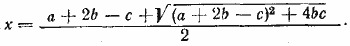
Расстояние y остается неопределенным. Величину х+с можно найти либо из вышеприведенного выражения, либо из уравнения 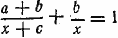 положив х+с = z. Получим уравнение положив х+с = z. Получим уравнение 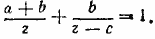
Берем только положительное решение.
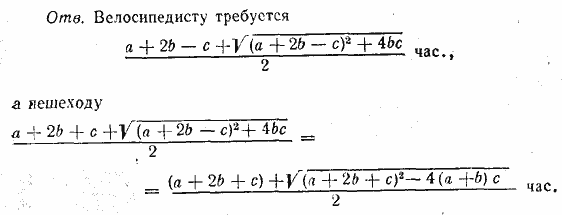
__________________________________________________
840. Обозначим длину пути (в километрах) через х. Согласно условию поезд А должен по расписанию нагнать поезд В через x/v час. после выхода. Фактически он нагнал поезд В, пройдя (x—а) км, т. е. через x—a/v час. Следовательно, оба поезда шли до встречи на a/v час. меньше положенного времени. Но поезд В должен был идти до встречи 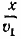 час, фактически же он прошел расстояние 2/3 х со скоростью v1 и расстояние 1/3 х — а со скоростью 1/2v1 затратив на весь этот путь час, фактически же он прошел расстояние 2/3 х со скоростью v1 и расстояние 1/3 х — а со скоростью 1/2v1 затратив на весь этот путь 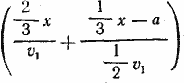 час. Следовательно, час. Следовательно,
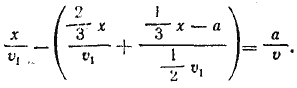
Отв. Длина пути равна 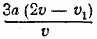 км. Задача имеет решение только при v1< 2v. км. Задача имеет решение только при v1< 2v.
__________________________________________________
841. Пусть сберкасса дает х%. Тогда первоначально было положено 1500/x руб. В начале второго года на счету вкладчика было 1500/x +15+85, т. е. ( 1500/x +100) руб. В конце второго года эта сумма обратится в ( 1500/x +100) (1 + x/100) руб. Получаем уравнение
( 1500/x +100) (1 + x/100) = 420
Отв. 300 руб.; 5%.
__________________________________________________
842. Обозначим производительность станков A, В, С соответственно через х, у, z. По условию
x = m/100(y + z) , y = n/100(x + z)
Найдем из этих уравнений выражения х и у через z; сложив их , получим
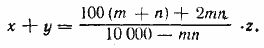
Искомое число процентов равно 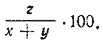 . .
Отв. 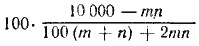
__________________________________________________
843. Примем за единицу измерения продукцию года, предшествующего первому. Тогда продукция 1-го года составит 1+ p/100.
По сравнению с ней продукция 2-го года возрастает на q%, т. е. на (1+ p/100 ) q/100 и составит
(1+ p/100 ) + (1+ p/100 ) q/100 = (1+ p/100 ) (1+ q/100 )
Если продукция 3-го года возрастает на х%, то она увеличивается
на (1+ p/100 ) (1+ q/100 ) x/100
По условию
1/3 [p/100 + (1 + p/100)q/100 + (1+ p/100 ) (1+ q/100 ) x/100]= r/100
Отв. 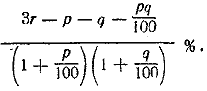
__________________________________________________
844. Пусть себестоимость всего товара составляет m руб. Тогда себестоимость первой проданной партии составляет а% от m, т. е. ma/100 руб. По условию полученная от продажи прибыль составляет р% этой суммы, т. е. ma/100• p/100 руб.
Себестоимость товара, оставшегося после продажи первой партии, равна
m— ma/100= т (1—a/100) руб.
Себестоимость второй проданной партии составляет b% от этой суммы, т. е.
т (1—a/100) b/100 руб.
При продаже второй партии было получено q% прибыли; следовательно, эта прибыль составляет
(1—a/100) b/100 • q/100 руб.
Себестоимость товара, оставшегося после второй продажи, составляет
m — ma/100— т (1—a/100) b/100 = m (1—a/100)(1—b/100) руб.
Пусть эта остальная часть продана с прибылью х%. Тогда прибыль от ее продажи составит
m (1—a/100)(1—b/100) x/100 руб.
Общая прибыль будет
т [a/100• p/100 + (1—a/100) b/100 • q/100 + (1—a/100)(1—b/100) x/100]
По условию общая прибыль должна составить r % от т руб., т. е. mr/100 руб.
Следовательно,
т [a/100• p/100 + (1—a/100) b/100 • q/100 + (1—a/100)(1—b/100) x/100] = mr/100
Величина т сокращается.
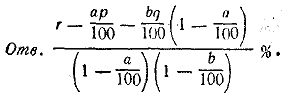
__________________________________________________
845. Первый способ. Положим, что каждый из отрезанных кусков весил х кг. Для краткости назовем первый сплав (весом т кг) «сплавом A», а второй — «сплавом В». Из двух вновь полученных слитков первый содержит (т—х) кг сплава А и х кг сплава В, а второй - х кг сплава А и (п—х) кг сплава В. По условию процентное содержание меди в обоих слитках одинаково. А это возможно лишь в том случае, когда в двух слитках количества сплава А и сплава В пропорциональны. Получаем уравнение
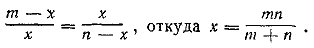
Второй способ. Пусть и кг есть вес меди в 1 кг сплава А, a v — вес меди в 1 кг сплава В. Тогда в первом слитке
(m—х) u + xv кг
меди, т. е. на 1 кг первого слитка приходится
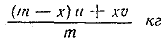
меди. Аналогично выразится вес меди, приходящийся на 1 кг второго слитка. Приравнивая два найденных выражения, получим уравнение
n[(m—x) u+xv] = m[(n—x) v+xu],
содержащее три неизвестных х, и, v. Его можно представить в виде
(и—v) (mx + nx— mn)=0.
По условию сплавы А и В имеют различные процентные содержания меди, т. е. величина и—v не может равняться нулю. Следовательно,
mx + nx— mn = 0.
Отв. Каждый кусок весил 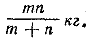
__________________________________________________
846. Пусть в первой кучке первоначально было x1 руб., во второй было x2 руб. и т. д.; в последней (n-й) кучке первоначально было хп руб. Первая кучка явно находится в особом положении, так как из нее сначала изымается 1/n чаcть и лишь в коние процесса она пополняется из п-й кучки, тогад как по отношению к каждой из остальных сначала производится пополнение из предыдущей кучки, а затем изъятие 1/n части. Поэтому рассмотрим какую- либо кучку, кроме первой. Обозначим ее номер через k. Первоначально в ней было хk руб., к ней прибавилось некоторое количество у руб. из (k—1)-й кучки, а затем из общей суммы у + хk руб. была изъята 1/n часть. Осталось 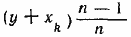 руб. По условию имеем уравнение руб. По условию имеем уравнение
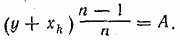 (1) (1)
В предыдущей же (k—1)-й кучке, если она не была первой (т. е. если k=/=2), должно было остаться А руб. (в первой кучке А руб. образуется лишь после пополнения ее из п-й кучки). Значит, до изъятия у руб. в ней было А+у руб. По условию изымаемая сумма у руб. составляет1/n часть от А+у , т. e.
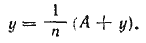 (2) (2)
Отсюда находим 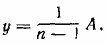 . Подставляя в (1), получаем хk= A . Подставляя в (1), получаем хk= A
Таким образом, во всех кучках, кроме, может быть, второй и первой (прежде исключенных из рассмотрения), первоначально было по A руб.;
x3 = x4 = ... = хn= А. (3)
Неизвестное x1 можно найти так. По условию сначала из суммы x1 руб. изымается 1/n часть. Остается 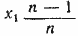 руб. В конце процесса в первую кучку добавляется некоторая сумма у руб. из последней кучки. Получаем уравнение руб. В конце процесса в первую кучку добавляется некоторая сумма у руб. из последней кучки. Получаем уравнение
 (4) (4)
Рассуждая (применительно к n-й кучке) так же, как выше, найдем,
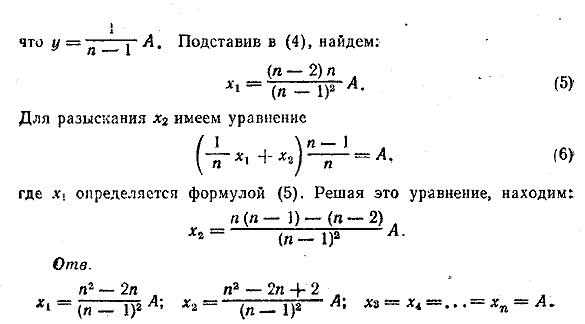
__________________________________________________
|