|
ГЛАВА 8
АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ
Ответы и решения
847. Пусть х — меньший из сомножителей. Тогда из условий задачи непосредственно вытекает, что
х (х+10) — 40 = 39х + 22
или
х2— 29х —62 = 0,
откуда x1 = 31, x2 =—2. Отрицательный корень отбрасываем, следовательно, множители равны 31 и 41.
__________________________________________________
848. До первой встречи первый велосипедист прошел s + а км, второй s — а км, где s — расстояние от А до В. До второй встречи они прошли соответственно
2s + 1/k s и 2s — 1/k s км.
Но если два тела движутся с постоянными скоростями, то отношение скоростей тел при равенстве затраченных времен равно oтношению пройденных телами путей. Поэтому для нахождения s имеем уравнение
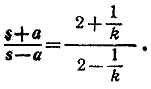
Отсюда s = 2ak км.
__________________________________________________
849. Если два тела движутся с постоянными скоростями, то на одном и том же участке пути отношение их скоростей обратно отношению затраченных телами времен. Пусть v—скорость третьей машины, t — время движения второй машины до того момента, когда ее обогнала третья. Тогда
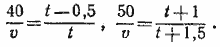
Разделив первое уравнение почленно на второе, найдем t = 3/2 часа; затем определим v = 60 км/час.
__________________________________________________
850. Пусть до встречи прошло х часов. Один и тот же путь от места встречи до пункта В велосипедист проехал за х часов, а пешеход прошел за x + t часов. Так как при равном пути времена , обратно пропорциональны скоростям, то

__________________________________________________
851. Обозначим расстояние от A до В через х, а расстояние от В до С через у. Тогда, учитывая, что время движения во всех случаях, о которых говорится в условиях задачи, одинаково, получим систему уравнений
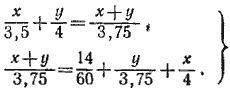
Решая эту систему, находим х = 14 км, у =16 км.
__________________________________________________
852. Пусть х—длина дороги по ровному месту, y —длина дороги в гору. Имеем систему уравнений
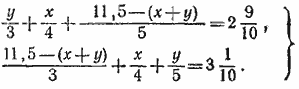
Сложив уравнения системы, найдем, что х = 4.
__________________________________________________
853. Обозначим через l расстояние между пунктами A и В и через v1,v2— скорости мотоциклов. За время t первый мотоцикл проехал путь, равный p+ l — q, а второй — путь q + l — р. Поэтому
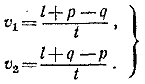 (1) (1)
С другой стороны, отношение скоростей равно отношению путей, пройденных до первой встречи, т. е.
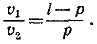
Подставив сюда v1 и v2 из (1), получим уравнение для определения l.
Решив его, найдем l = 3р — q.
Подставив это значение l в формулы (1), получим:
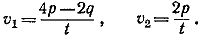
__________________________________________________
854. Разность между временами опоздания самолета в первом и втором рейсахравная 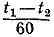 часов, связана с тем, что путь в d км был пройден с разными скоростями: в первом рейсе скороcть была v км/час, во втором w км/час (на остальных участках пути скорости были соответственно равны). Отсюда получаем уравнение часов, связана с тем, что путь в d км был пройден с разными скоростями: в первом рейсе скороcть была v км/час, во втором w км/час (на остальных участках пути скорости были соответственно равны). Отсюда получаем уравнение
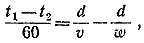
из которого находим, что начальная скорость самолета равна
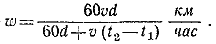
__________________________________________________
855. Пусть отношение весов сплавляемых кусков равно α : β. Тогда
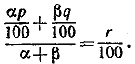
Отсюда получаем:
α : β = (r — q) : (p — r).
Решение возможно, если р > r > q или р < r < q.
Чтобы найти максимальный вес нового сплава, рассмотрим отношения 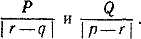
Ecли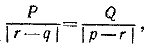 максимальный вес равен максимальный вес равен
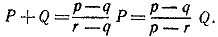
Если 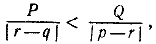 , то максимальный вес равен , то максимальный вес равен
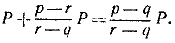
Если, наконец, 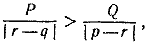 то максимальный вес равен то максимальный вес равен
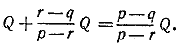
__________________________________________________
856. Пусть каждый рабочий работал по t дней и пусть A заработал х рублей, а В заработал у рублей. Из условий задачи получаем систему уравнений
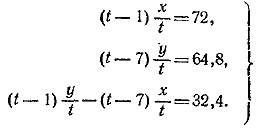 (1) (1)
Из первых двух уравнений находим:
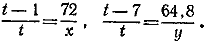
Тогда из последнего уравнения получаем:
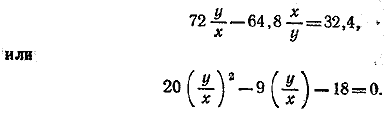
Отсюда y = 5/6 x (отрицательный корень отбрасываем). Деля теперь второе уравнение системы (1) на первое и заменяя y/x его значением, находим:
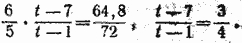
Отсюда t = 25 и, следовательно,
х = 75 руб., у = 90 руб.
__________________________________________________
857. Обозначим через t1 время, прошедшее до первой встречи, через t2— время, прошедшее до второй встречи, и через R —рaдиус окружности. За время t1 первое тело прошло путь vt1 а втoрое - путь 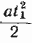 . Сумма этих путей равна длине окружности, так что . Сумма этих путей равна длине окружности, так что
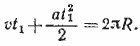 (1) (1)
За время t2 каждое тело прошло один и тот же путь, равный длине окружности, так что
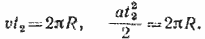
Исключая отсюда t2, найдем 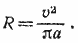 . Подставив это значение R в (1), получим квадратное уравнение относительно t1 . Подставив это значение R в (1), получим квадратное уравнение относительно t1
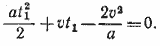
Решив это уравнение и отбросив отрицательный корень (так как по смыслу задачи должно быть t1 > 0), окончательно получим:
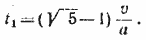 . .
__________________________________________________
858. Обозначим через q1 и q2 производительности кранов (в л/мин) и через v — объем бассейна. Время наполнения бассейна каждым из кранов будет равно
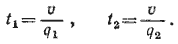 (1) (1)
Первое условие задачи приводит к уравнению
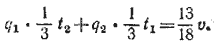
Используя равенства (1), получим квадратное уравнение
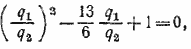
решениями которого будут 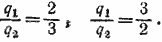 Из второго условия задачи следует: Из второго условия задачи следует:
v =(3•60 + 36)( q1 + q2 ) = 216( q1 + q2 ).
Из (1) находим искомые величины:
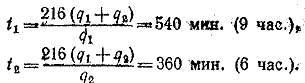
Есть и второе решение:
t1 = 360 мин., t2 = 540 мин.
__________________________________________________
859. Обозначим через γ удельный вес воды, а через s — площадь поперечного сечения трубки. Атмосферное давление ра найдется по формуле
ра = γ с.
Если ра—давление под поршнем в поднятом положении, то, по закону Бойля—Мариотта, для воздуха, заключенного между поршнем и уровнем воды, имеем
p1(b — x)s = раhs (рис. 2).
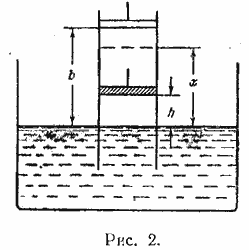
Уравнение равновесия столба жидкости имеет вид ра — p1 = γx Это приводит к уравнению
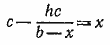
( γ сокращается), т. е. к квадратному уравнению
х2 — (b + c)х + (b — h)c = 0.
Отсюда находим:
x = 1/2 [(b + c) — √(b — c)2 + 4hc].
__________________________________________________
860. Пусть p1 и p2 — давления воздуха, находящегося под поршнем, в положениях I и II соответственно (рис. 3) и γ — удельный вес ртути.
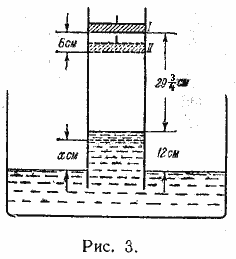
Уравнения равновесия столбов ртути высотой 12 см и х см будут соответственно
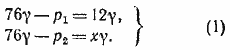
Закон Бойля—Мариотта для воздуха, находящегося под поршнем, дает уравнение
p1293/4 = p2(36— x).
Подставив сюда выражения для p1 и p2 из (1), получим квадратное уравнение для x:
293/4• 64 = (76 — x)(36 — x),
или
х2 — 112х +832 = 0.
Отсюда х = 56± √3136 — 832 = 56 ± √2304 = 56 ± 48, т. е. х = 8 см.
__________________________________________________
861. Пусть часы спешат на х минут в сутки. Тогда они покажут верное время через 2/xсуток. Если бы они показывали на 3 минуты меньше, а спешили бы на х + 1/2 минут в сутки, то верное время они показали бы через 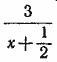 суток. Следовательно, суток. Следовательно,
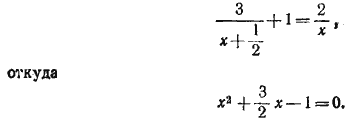
Решая это уравнение, найдем х = 0,5.
__________________________________________________
862. Если х — исходные суммы вкладчиков, а у — процент, выплачиваемый сберкассой, то
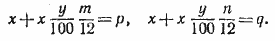
умножая первое уравнение на п, второе на т и вычитая из первого второе, найдем:
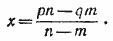
возвращаясь снова к первоначальной системе и вычитая из первого уравнения второе, получим:

__________________________________________________
863. Обозначим через v1 и v2 скорости точек, и пусть v1 > v2. Первое условие задачи запишется уравнением
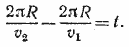
Второе условие означает, что за время Т точка, движущаяся с большей скоростью, пройдет по окружности путь на 2πR больший, чем другая точка. Это дает второе уравнение
Тv1—Тv2 = 2πR.
Из второго уравнения находим:
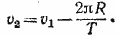
Подставив это выражение для v2 в первое уравнение, получим квадратное уравнение для v1:
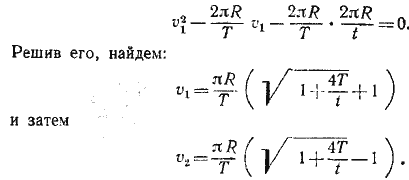
__________________________________________________
864. Пусть v —объем раствора в колбе, х — количество соли, содержащейся в растворе, в процентах. В пробирку отливают v/n раствора и выпаривают до тех пор, пока процентное содержание соли не повысится вдвое. Так как количество соли при этом не изменяется, то, следовательно, объем раствора в пробирке уменьшится вдвое и вес выпаренной воды будет равен v/2n.
После переливания выпаренного раствора обратно в колбу в колбе снова будет то же количество соли, что и раньше, т. е. v x/100 , а объем раствора уменьшится на v/2n. Отсюда получаем уравнение
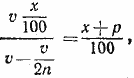
из которого находим:
х = (2n — 1)р.
__________________________________________________
865. Пусть в первом сосуде было х литров спирта; тогда во втором будет 30—х литров. После доливания первого сосуда водой в 1 л полученной смеси содержалось x/30 спирта и 1— x/30 воды.
После переливания из первого сосуда во втором стало 30 — х + x/30 x литров спирта и ( 1— x/30 )х литров воды. Эта новая смесь такова, что в одном литре смеси содержится
1— x/30 +(x/30)2 литров спирта.
После того, как 12 л новой смеси было отлито в первый сосуд, в нем оказалось
12 [1— x/30 +(x/30)2] + x/30(30—х) литров спирта,
а во втором сосуде
18 [1— x/30 +(x/30)2] литров спиртаю
По условию
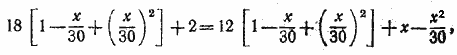
откуда получаем уравнение
x2 —30х +200 = 0.
Это уравнение имеет корни
x1 =20, x2=10.
Итак, в первом сосуде было либо 20 л (и тогда во втором 10 л), либо 10 л (и тогда во втором 20 л).
__________________________________________________
866. Пусть х — расстояние от первого берега до того места, где С покинул лодку. Заметим сначала, что на таком же расстояний от второго берега А сел в лодку. Действительно, способ, которым преодолели переправу А и С, отличается лишь тем, что С сначала ехал в лодке, а затем плыл, а А—наоборот. Так как они плывут с одинаковой скоростью v, причем v=/= v1, и затрачивают одинаковое время на переправу, то, очевидно, указанные расстояния должны быть равны.
После этого замечания легко составить уравнение
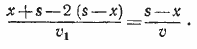
Здесь левая часть выражает время, затраченное лодкой на преодоление пути до встречи с A, а правая часть — время, которое затратил A до встречи с лодкой.
Из полученного уравнения находим:
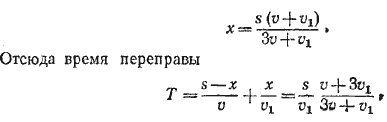
Примечание, Можно было бы решить задачу и без предварительного замечания о равенстве указанных выше расстояний. При этом, однако, пришлось бы ввести несколько неизвестных и решение оказалось бы более громоздким.
__________________________________________________
|