|
ГЛАВА 8
АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ
Ответы и решения
867. Обозначим искомое расстояние через s км, скорость поезда через v км/час. За 6 часов до остановки, вызванной снежным заносом, поезд прошел 6v км, а оставшуюся часть пути длиной (s— 6v) км он прошел за 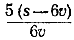 часов, так как скорость поезда на этом участке пути была равна 5/6 v. часов, так как скорость поезда на этом участке пути была равна 5/6 v.
Поезд был в пути всего (с учетом двухчасовой вынужденной стоянки) 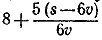 часов. Это число часов на один час больше положенных по расписанию s/v часов. Таким образом, получаем уравнение часов. Это число часов на один час больше положенных по расписанию s/v часов. Таким образом, получаем уравнение
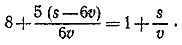
Проведя аналогичное рассуждение относительно второго поезда, составим еще одно уравнение:
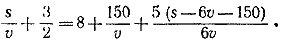
Из этой системы находим s = 600 км.
__________________________________________________
868. Обозначая через v скорость лодки в стоячей воде, а через w скорость течения, получим систему двух уравнений
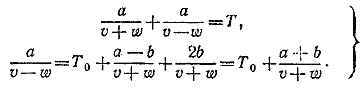
Решая эту систему относительно неизвестных 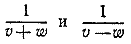 и беря обратные величины, находим: и беря обратные величины, находим:

Отсюда следует, что
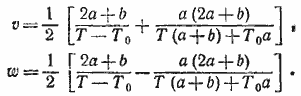
__________________________________________________
869. Пусть х—время, в течение которого был открыт второй кран, v—скорость поступления воды из первого крана, w—скорость поступления воды из второго крана (v и w измеряются в м3/час). Имеем:
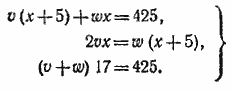
Из второго и третьего уравнений получаем:
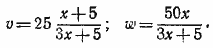
Подставляя эти выражения в первое уравнение, находим:
3х2—41х—60 = 0,
откуда х=15 час. (Второй корень, отрицательный, не годится.)
__________________________________________________
870. Обозначим искомую скорость поезда через v км/час, а скорость поезда по графику—через v1 км/час. Первую половину пути поезд проходил за 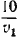 часов, на преодоление второй половины и на стоянку поезд затратил в первый раз часов, на преодоление второй половины и на стоянку поезд затратил в первый раз 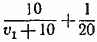 часов и во второй раз часов и во второй раз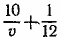 часов. Но оба раза поезд пришел в В вовремя, часов. Но оба раза поезд пришел в В вовремя,
и поэтому
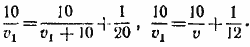
Из первого уравнения найдем v1:
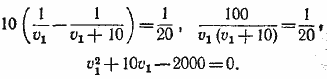
Это уравнение имеет только один положительный корень v1 = 40. Из второго уравнения найдем, что v = 60 км/час.
__________________________________________________
871. Пусть расстояние АВ равно s км, а скорости первого и второго самолетов равны v1 и v2. Тогда, в силу условий задачи, имеем систему трех уравнений:
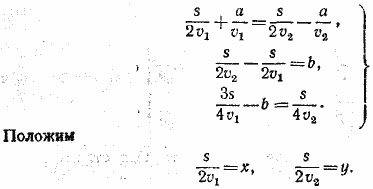
Из второго и третьего уравнений найдем: х = 3/2b, y = 5/2b, а из первого: 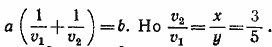 Теперь уже нетрудно найти, что Теперь уже нетрудно найти, что 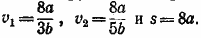
__________________________________________________
872. Пусть u — скорость катера в стоячей воде, а v —скорость течения. Тогда имеем систему
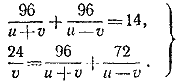
Для ее решения положим u/v = z. Умножив обе части второго уравнения на v , найдем:
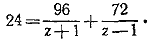
Освобождаясь от знаменателей, получаем:
24z2—168z = 0.
Так как z =/= 0, то z = 7. Следовательно, u = 7v. Подставляя u = 7v в первое уравнение системы, находим:
96/8v + 96/6u =14
откуда
v =2 км/час, u =14 км/час.
__________________________________________________
873. Путь, пройденный каждым телом за t сек, определяется формулой
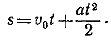
Чтобы найти v0 и а для каждого тела, подставляем в эту формулу приведенные в условиях задачи числовые данные:
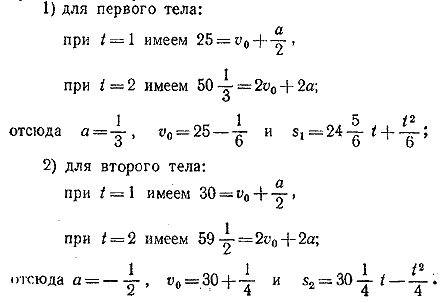
В тот момент, когда первое тело нагонит второе, будет s1 = s2 + 20; отсюда получаем квадратное уравнение для определения t:
t2 —13t — 48 = 0.
Решая его, находим t = 16. Второй, отрицательный, корень отбрасываем.
__________________________________________________
874. Пусть v — собственная скорость лодки. Тогда время движения лодки равно
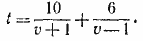
По условию имеем:
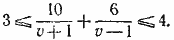 (1) (1)
Необходимо, чтобы было v > 1, так как в противном случае лодка не сможет двигаться против течения. От системы неравенств (1) перейдем к равносильной системе неравенств
3(v2 — 1) < 16v — 4 < 4(v2 — 1).
Итак, нужно, чтобы сразу выполнялись два неравенства:
3v2— 16v + 1 < 0
и
4v2 —16v > 0.
Первое неравенство удовлетворяется, если
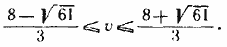
Второе неравенство удовлетворяется, если v < 0 или v > 4. Но так как v > 1, то окончательно имеем:
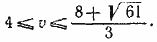
__________________________________________________
875. Обозначим через x объем воды в сосуде A до переливания. Тогда первоначальный объем воды в сосудах В и С будет равен соответственно 2х и 3х, а общий объем х + 2х + 3х = 6х.
После первого переливания из A в В и из B в С глубина во всех сосудах стала одинаковой, и поэтому объемы воды относятся как площади основания, т. е. как 1 : 4 : 9. Поэтому после первого переливания объемы воды в сосудах А, В, С будут соответственно иметь значения
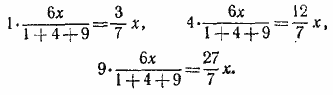
После второго переливания из С в В эти объемы станут соответственно равными
3/7 x , 12/7 x + 128 4/7 , 27/7 x —128 4/7
После третьего переливания из В в А объем воды в А стал равным х—100, а в В —равным
1/2(x— 100)•4 = 2(x —100).
Сложив объемы воды во всех сосудах, получаем уравнение первой степени относительно х:
(х— 100) + 2 (х— 100) + 27/7 х— 128 4/7 = 6х.
Решая это уравнение, находим:
х = 500.
Итак, первоначальное количество воды во всех сосудах таково:
в А— 500 л,
в B — 1000 л,
в С— 1500 л.
__________________________________________________
876. Пусть искомое число имеет вид xyzt (здесь буквы х, у, z, t обозначают цифры соответствующих разрядов). По условиям задачи получаем следующую систему:
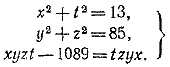 (1) (1)
В силу поразрядного вычитания в третьем уравнении системы (1) либо t= 9, либо
(10 + t )— 9 = х,
т. е.
x = t + 1. (2)
Но из первого уравнения системы (1) следует, что t < 4 и поэтому имеет место (2). Тогда из первого уравнения системы (1) получаем уравнение для определения t :
(t + 1)2 + t 2 =13,
откуда
t = 2.
Из (2) следует теперь, что х = 3, и третье уравнение системы (1) принимает вид
3yz2— 1089 = 2zy3. (3)
Заметим далее, что z < 9 (если z = 9, то из (3) следует, что у = 0, но тогда не удовлетворяется второе уравнение системы (1)).
Из (3) находим:
(z —1 + 10) — 8 = y,
т. е.
z = у —1. (4)
Наконец, из второго уравнения системы (1) и (4) определяем z = 6, у = 7. Итак, искомое число есть 3762.
__________________________________________________
877. Сначала найдем расстояние х от начала до места первой встречи. Уравнение времен движения обоих точек имеет вид

От начала движения до первой встречи прошло время, равное
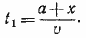
Подставив сюда найденное значение х, получим:
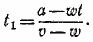
Пусть τ —интервал времени между двумя последовательными встречами. Тогда

Последовательные встречи будут происходить в моменты времени t1, t1+ τ, t1+ 2τ, ... Момент n-й встречи будет
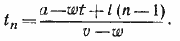
__________________________________________________
878. Удельный вес первого из составляющих сплав металлоз обозначим через γ1 , второго—через γ2 и воды — через γ. Пусть х—вес первого металла в сплаве. По закону Архимеда потеря веса сплава в воде равна
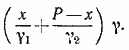
Аналогично для чистых металлов эта потеря будет равна
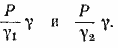
Эти потери даны и равны соответственно В и С. Отсюда находим:
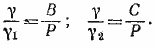
Следовательно, потеря веса сплава равна
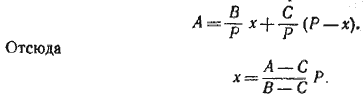
Для разрешимости задачи необходимо, чтобы В =/= С. Далее из того, что x/P есть число, заключенное между 0 и 1, вытекает неравенство
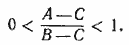
Отсюда следует, что либо В > А > С, либо С > А > В. Итак, для того чтобы задача имела решение, необходимо и достаточно, чтобы число А было заключено между числами В и С.
__________________________________________________
879. Обозначим расстояние от пункта А до устья реки через s, расстояние от устья реки по озеру до пункта В — через s1 скорость парохода (без буксировки) —через v, скорость течения реки через v1.
Нужно определить 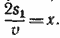 . .
Из условий задачи составляем три уравнения:
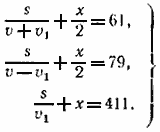
Из первого уравнения имеем:
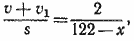 (1) (1)
из второго уравнения найдем:
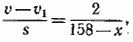 (2) (2)
из третьего уравнения получим:
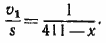 (3) (3)
Вычитая из равенства (1) равенство (2) и используя равенство (3), получим уравнение относительно х:
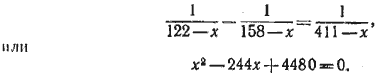
Решая это уравнение, находим:
x1=20, x2 = 224.
Очевидно, значение x2 = 224 не подходит, так как в уравнении (1) левая часть не может быть отрицательна.
__________________________________________________
880. Обозначим расстояние АВ через s, расстояние ВС — через s1; пусть, далее, v —скорость лодки, v1—скорость течения (предполагается, что s и s1 выражены в одних и тех же единицах длины; v и v1 —скорости, рассчитанные на час).
Для движения лодки вниз по течению от A до С имеем:
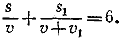 (1) (1)
Для движения лодки вверх по течению от С до A имеем:
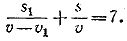 (2) (2)
При условии, что на АВ течение такое же, как и на ВС, путь АС займет
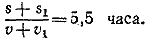 (3) (3)
Нужно определить отношение 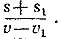 . .
Приведем уравнения (1), (2) и (3) к общему знаменателю и, умножив обе части уравнения (3) на v =/= 0, получим систему
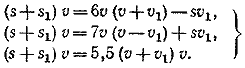 (4) (4)
Сложив первые два уравнения и используя третье, получим:
2(s + s1) v = v (13v—v1) = 11v(v + v1).
Отсюда v = 6v1 Но из третьего уравнения системы (4) имеем 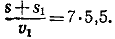 . .
Следовательно,
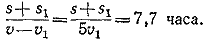
__________________________________________________
881. Обозначим через v объем сосуда, и пусть α1 — процентное содержание кислоты в нем после первого перемешивания, α2— процентное содержание кислоты после второго перемешивания и т. д. Имеем:
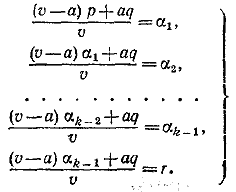
Умножая s-e равенство на 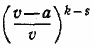 и складывая, получаем: и складывая, получаем:
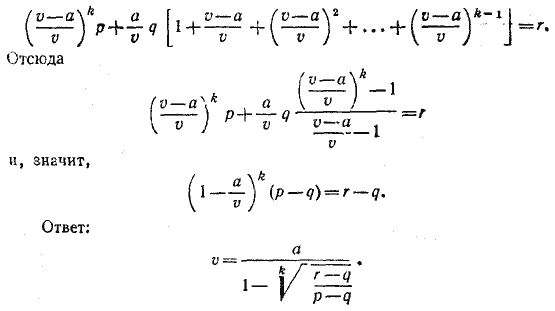
__________________________________________________
882. В конце первого года вклад возрос на Ap/100 рублей, а вкладчик взял В рублей. Поэтому к началу второго года вклад составил в рублях сумму
P1 = A(1+ p/100) — В
В конце второго года вклад составил сумму
P2 = P1 (1+ p/100) — В = A(1+ p/100) 2 — В [ 1 + (p/100 + 1 )]
а в конце третьего года
Р3 = Ak3 — В ( l + k + k2 ), где
k = 1+ p/100.
Очевидно, в конце n-го года сумма вклада будет равна
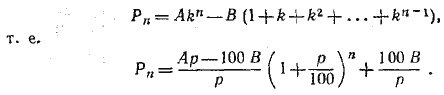
По условию задачи нужно найти такое п, чтобы Рn > 3А. Тогда
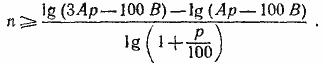
Задача имеет смысл, если сумма вклада возрастает, т. е. если
Ар> 100 В.
Так как, кроме того, р > 0, А > 0, В > 0, то выражение, стоящее в правой части неравенства (1), имеет смысл.
__________________________________________________
883. В конце первого года на лесной делянке древесины было
a(1+ p/100) — x = a1
к концу второго года —
a1(1+ p/100) — x = a2
к концу третьего года —
a2(1+ p/100) — x = a3
и т.. д. Наконец, к концу n-го года было
an —1(1+ p/100) — x = an= аq
древесины. Нужно определить х.
Положив для сокращения записи 1+ p/100 = k из последнего уравнения получим
x = kan —1 —aq. Из предыдущего уравнения выразим an —1 Получим:
x= k (kan —2—х)—aq = k2an —2—kх—aq.
Но
an —2 = kan —3—x.
Следовательно,
x = k3an —3 — k2x — kx — aq.
Продолжая далее таким же образом, мы выразим, наконец, a2 через a1 и получим следующее уравнение относительно х:
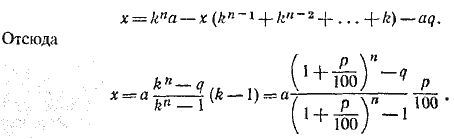
__________________________________________________
884. До переливания концентрация qi спирта была равна:
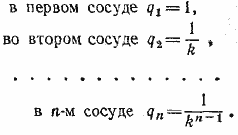
Пусть после всех переливаний концентрации стали равны соответственно: p1, p2, ..., pn . Тогда p1 = 1, а p i при i > 1 определяется из уравнения
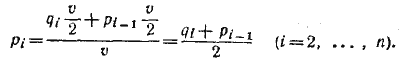
Это уравнение мы получаем, деля количество спирта
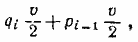
которое оказывается в i-м сосуде при переливании из ( i— 1)-го сосуда, на объем всего сосуда v. Таким образом,
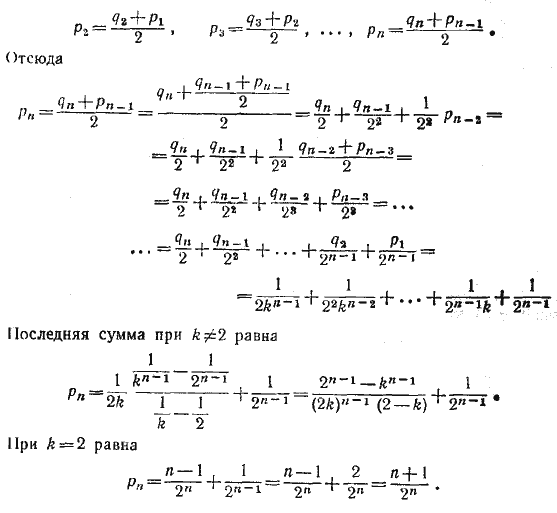
__________________________________________________
885. Дробь имеет вид 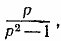 , где р — целое, большее нуля. Условия задачи записываются в виде неравенств , где р — целое, большее нуля. Условия задачи записываются в виде неравенств

Преобразуем первое неравенство к виду
3(р + 2) > р2 + 1 или 0 > р2 — 3р —5.
Решая соответствующее квадратное уравнение, получим:
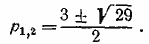
Из неравенства 0 > р2 — 3р —5 получаем р2 < р < р1. Но р2 < 0, а р > 0, поэтому
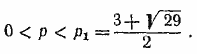
Легко видеть, что р1 лежит между 4 и 4,5. Следовательно, из этого неравенства вытекает, что р, как число целое, может принять только одно из четырех значений: р =1, 2, 3, 4. Подставляя эти значения во второе неравенство
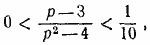
находим, что р =/=1, р =/=2 и р =/=3. Таким образом, 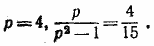
__________________________________________________
|