ГЛАВА 9

РАЗНЫЕ ЗАДАЧИ

Алгебраические преобразования

Ответы и решения

886. Имеем:

__________________________________________________

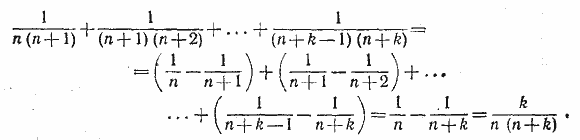
887. Пусть сначала х =/= а. Умножая и деля исследуемое произведение на х — а и применяя последовательно формулу для разности квадратов двух чисел, получим:

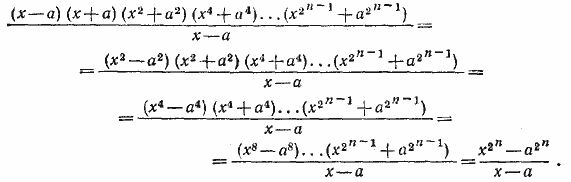
Пусть теперь х = а. Тогда исследуемое произведение равно

__________________________________________________

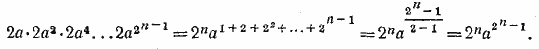
888. Умножим   и   разделим   данное выражение на произведение

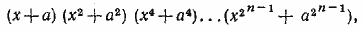
которое   при   всех  вещественных  х =/= —а  отлично  от нуля.   

 Легко видеть, что результат можно записать следующим образом:

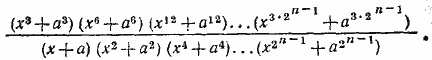
В числителе и знаменателе этой дроби стоят произведения, аналогичные уже рассмотренному в предыдущей задаче. Поэтому, умножая числитель и знаменатель на произведение (х — а) (х³ — а³), мы приведем наше выражение к виду

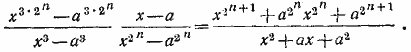
Наш метод теряет силу при х = ±а. В этих случаях, однако, простой подсчет показывает, что при х = —а произведение равно 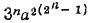, a при х = а оно  оказывается равным

__________________________________________________

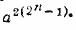
889. Очевидно,

S_k—S_k—1 = b_k                     (k= 2, 3, 4,  ..., п)   (1)

и

S₁  =  b₁ .                                              (2)

Подставляя в сумму

a₁b₁ +  a₂b₂  + ... + a_nb_n

вместо  b₁,  b₂ ....  b_n    их значения,  из (1) и  (2) получим:

__________________________________________________

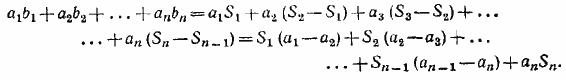
890. Умножив обе части равенства на 2,   перенесем его правую часть влево. После простых преобразований получаем:

2(а² + b² + c² — аb—ас—bс) =   а²—2аb + b²   + а² — 2ас + c²   + b² — 2bс + c²  =

= (а — b)² + (а — с)² + (b — с)²=0.

Так как а, b, с вещественны, то это возможно только тогда, когда а = b =с.

__________________________________________________

891. Умножим   а² + b² + c² — bc — ca — ab    на   a + b + с.    После несложных   подсчетов  находим,   что  произведение  равно  а³ + b³ + c³ — 3abc,   т.   е.,   согласно условию задачи, равно нулю. Отсюда вытекает справедливость утверждения задачи.

__________________________________________________

892. Так как р =/= 0, q =/=0, то можно написать:

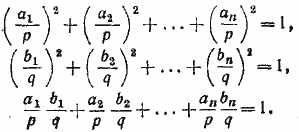
Складывая  первые  два из этих равенств и вычитая   удвоенное третье, находим:

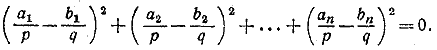
Принимая во внимание вещественность всех величин, заключаем, что

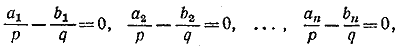
откуда непосредственно вытекает утверждение задачи.

__________________________________________________

893. Положим р_n = а_n—а_n—1. Тогда из условия задачи следует формула  р_n = p_n—1+ 1, показывающая, что числа р_n образуют арифметическую   прогрессию   с   разностью   1.   Поэтому   р_n = р₂ + п —2. Теперь находим:

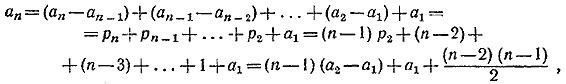
или окончательно

__________________________________________________

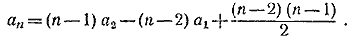
894. Первое  решение.   Заданное соотношение можно переписать в двух видах

а_n— αа_n—1= β (а_n—1— αа_n—2),

а_n— βа_n—1= α (а_n—1— βа_n—2).

Полагая а_n— αа_n—1 = и_n,    а_n— βа_n—1 = v_n, найдем, что

и_n = β и_n—1   ,       v_n = α v_n—1.

Из последних соотношений следует, что

и_n = β^n—2 и₂   ,       v_n = α^n—2 v₂.

ИЛИ

а_n— αа_n—1= β^n—2(а₂— αа₁)

а_n— βа_n—1= α^n—2(а₂— βа₁)

Исключая отсюда а_n—1, получим окончательно

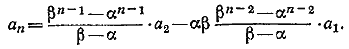
Второе  решение. Полагая в исходном соотношении   п последовательно равным 3, 4....,найдем

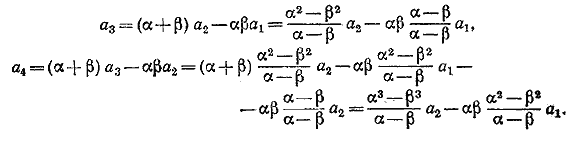
Общую формулу

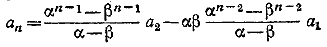
легко теперь доказать методом полной индукции.

__________________________________________________