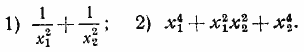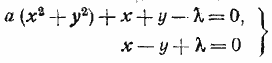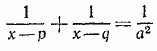ГЛАВА 9

РАЗНЫЕ ЗАДАЧИ

Теорема Безу, свойства корней многочленов

В отдельных зaдaчах используются формулы Виета, связывающие коэффициенты уравнения третьей степени

x³  + px² + qх + r = 0         (1)

с его корнями x₁ , x₂ , x_{3 .}  Они имеют вид:

x₁ + x₂ + x₃ = — p,   x₁x₂ +  x₂ x₃  + x₃x₁  =  q,   x₁ x₂ x₃ =  — r   (2)

Формулы (2) находятся приравниванием коэффициентов при одинаковых степенях х в тождестве

x³  + px² + qх + r = ( x — x₁)( x — x₂)( x — x₃)

*************************************

895.     Корни x₁ и x₂ уравнения x²—3аx + a² = 0 таковы, что x₁² + x₂²= 1,75. Определить а.  Решение

896.  Дано уравнение x²  + px + q = 0 . Составить квадратное уравнение, корнями которого были бы

y₁ = x₁² + x₂²       y₂ = x₁³ + x₂³  Решение

897.  Пусть x₁ и x₂ — корни уравнения

ax²  + bx + c = 0    (aс=/=0).

Не   решая   уравнения,   выразить   через   его   коэффициенты величины:

Решение

898.   Каким условиям должны   удовлетворять вещественные коэффициенты   a₁, b₁, a₂, b₂, a₃, b₃, чтобы   выражение

(a₁ + b₁x) ² + (a₂ + b₂x) ² + (a₃ + b₃x) ²

было квадратом многочлена первой степени относительно x с вещественными коэффициентами?

Решение

899.   Доказать,   что   корни квадратного уравнения  x²  + px + q = 0    с   действительными   коэффициентами   отрицательны или имеют отрицательную вещественную часть тогда и только тогда, когда р > 0, q > 0.

Решение

900.   Доказать, что если оба корня  уравнения

 x²  + px + q = 0

положительны, то корни уравнения qy² + (p — 2rq)y + 1 — рr = 0 положительны при всех r  > 0. Выяснить, справедливо ли это утверждение при r <  0. Решение

901.   Найти все действительные значения р, при которых корни уравнения

(р — 3) x² — 2рх + 6р =  0

вещественны и положительны. Решение

902.   При любом  положительном   λ все  корни уравнения

ax²  + bx + c + λ = 0

вещественны и положительны. Доказать, что в этом случае а = 0 (коэффициенты a, b и с предполагаются вещественными). Решение

903.   Доказать, что   оба корня уравнения x² + x + 1 = 0 удовлетворяют уравнению

x^3m + x³ⁿ⁺¹ + x^3p+2=0

где т, п и р —любые целые числа. Решение

904.  Система уравнений

имеет вещественные решения при любом λ. Доказать, что а = 0. Решение

905.   Доказать, что при любых   вещественных значениях а,  p, q  уравнение

имеет вещественные корни. Решение

906.   Доказать, что квадратное уравнение

а²х² + (b² + а² — с²) х + b² = 0

не   может   иметь   вещественных   корней,   если   a + b > c   и  |а — b| < с. Решение

907.   Известно, что x_{1  ,} х₂,  x₃   —корни уравнения

x³ — 2x² + х + 1 =0.

Составить новое уравнение, корнями которого были бы числа

y₁ = х₂x₃ ,   y₂ = x₃ x₁ ,   y₃ = x₁х₂,

Решение

908.   Известно, что x_{1  ,} х₂,  x₃ — корни уравнения

x³ — x²  — 1 = 0.

Составить новое уравнение, корнями которого были бы числа

y₁ = х₂+x₃ ,   y₂ = x₃ + x₁ ,   y₃ = x₁+ х₂

Решение

909.  Выразить свободный член с кубического уравнения

x³ + ax²  + bx + c = 0

через коэффициенты а и b, зная, что корни уравнения образуют арифметическую прогрессию. Решение

910.   Пусть   известно, что   все   корни   некоторого  уравнения

x³ +px² +qx + r = 0

положительны. Какому дополнительному условию должны удовлетворять его коэффициенты р, q, r для того, чтобы из отрезков, длины которых равны этим корням, можно было составить треугольник?

Указание.   Рассмотреть выражение

(x₁ + x₂—x₃) (x₂+x₃—x₁) (x₃ + x₁—x₂).

Решение

911.   Уравнения

x³ +p₁x +q₁  = 0,

x³ +p₂x +q₂ = 0

(p₁=/=p₂, q₁=/=q₂)  имеют общий корень. Найти этот корень, а также остальные корни обоих уравнений. Решение

912.   Найти все значения λ, при которых два уравнения

λx³ — x² — х — (λ+1) = 0,

λx² — х — (λ+ 1) = 0

имеют общий корень, и найти этот корень. Решение

913.Все корни многочлена

Р(х) = x³ +px +q

с  действительными   коэффициентами   и q=/=0  вещественны. Доказать,  что р < 0.

Решение

914.   Доказать, что уравнение

x³ + аx² — b = 0,

где а и b вещественны и b >0, имеет один и только один положительный корень.

Решение

915.   Найти все вещественные значения а и b , при которых уравнения

x³ + аx²+18 = 0,

x³ + bx² +12 = 0

имеют два общих корня, и определить эти корни. Решение

916.   Доказать,  что

Решение

917.   Пусть  a,   b,   с —попарно   не   равные   между собой числа. Доказать, что выражение

а² (с—b) + b²(а — с) + с²(b — а)

не равно нулю.  Решение

918.   Разложить на множители выражение

(x + y + z)³ — x³ —у³ — z³.

Решение

919.   Доказать, что если три вещественных числа а, b, с связаны соотношением

то обязательно какие-либо два из этих  чисел равны по абсолютной величине и противоположны по знаку. Решение

920.    Выяснить, при каких  комплексных значениях р и q двучлен х⁴—1 делится на квадратный трехчлен x²  + px + q. Решение

921.     При каких значениях а и п многочлен х^п — ax^п—1+ ах—1 делится на (х—1)²?

Решение

922.   Многочлен  р(х)  дает   при делении на х — а остаток А, при  делении  на              х — b — остаток  В, при делении на х — с —остаток С. Найти многочлен, получающийся в остатке при   делении    р(х)  на   (х — а)(х — b )(х — с),   предполагая, что среди чисел а, b и с нет равных. Решение