|
|
ГЛАВА 9 РАЗНЫЕ ЗАДАЧИ Наибольшие и наименьшие значения
930. Пусть r(t) —расстояние между поездами в момент времени t. Тогда r2(t) = (а — v1t)2 + (b — v2t)2 = (v12 + v22)t2 — 2(av1 + bv2)t + a2 + b2 Заметим, что если r2(t) имеет наименьшее значение при t = t0, то и r(t) также принимает наименьшее значение при t = t0. Верно и обратное. Задача сводится к нахождению наименьшего значения квадратного трехчлена r2(t). Согласно формуле (4) наименьшее значение r2(t), а следовательно и r(t), достигается в момент времени
Используя далее формулу (3), находим наименьшее расстояние между поездами:
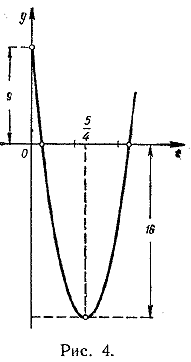
__________________________________________________ 931. В момент времени t автомашина находится на расстоянии 40 t км от пункта А, а мотоцикл—на расстоянии 32/2 t2 + 9 км от того же пункта. Следовательно, расстояние между ними равно абсолютной величине разности 16t2 + 9—40t. Обозначая эту разность через у (t), начертим график квадратного трехчлена у (t) (рис. 4). Он представляет собой параболу, которая пересекает ось t при t1 = 1/4 и t2 = 21/4. Из графика ясно, что наибольшая по абсолютной величине ордината у при условии 0< t<2 соответствует вершине параболы. Вершина параболы лежит на оси симметрии, которая пересекает ось t в точке
Таким образом, наибольшее расстояние достигается через 1 час 15 минут после начала движения и равно 16 км. __________________________________________________ 932. Обозначим исследуемое выражение через у и преобразуем его следующим образом: у = log24 x + 12 log22 x (log2 8— log2 x) = = log22 x(log22 x—12 log2 x + 36) = log22 x (6 — log2 x)2. Положим, далее, log2 x = z, так что 0 < z < 6. Тогда задача сводится к нахождению наибольшего значения переменной y = z2 (6 — z)2. Достаточно найти наибольшее значение для z (6 — z) при условии 0 < z < 6, так как чем больше положительное число, тем больше и его квадрат. Квадратный трехчлен z (6 — z) = — (z—3)2 + 9 достигает наибольшего значения при z = 3. Таким образом, наибольшее значение достигается при z = 3 и равно 81. __________________________________________________ 933. Первое решение. Очевидно, достаточно рассматривать лишь положительные значения х. Согласно известному неравенству (3), имеем:
Следовательно, для всех х > 0
Так как (1) превращается в равенство при условии ах2= b, то при
В силу (2) это и есть наибольшее значение функции. Второе решение. Разрешив соотношение
относительно х, получим:
Из формулы (5) следует, что при всех вещественных х должно выполняться неравенство 1—4aby2 > 0. Отсюда
Так как значение __________________________________________________ 934. Путем очевидных преобразований получаем
В силу неравенства (3)
причем знак равенства в (1) имеет место только в случае, когда
Таким образом, при всех х0 > 0
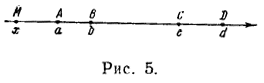
и знак равенства в этой формуле имеет место при х = √2 —1 __________________________________________________ 935. Возьмем числовую ось и отметим на ней точки А, В, C, D, соответствующие числам а, b, с и d. Точку с переменной абсциссой
x будем обозначать через М (рис. 5). Рассмотрим следующие пять случаев. 1) x < а; тогда φ(x) = MA + MB + MC+MD = AB + 2MB + 2BC + CD. Отсюда ясно, что φ(x) будет принимать наименьшее значение в том случае, когда точка М совпадает с точкой А, и что это значение равно 3AB + 2BC + CD. 2) а < х < b; тогда φ(x) = AM + MB + MC + MD = AB + 2MB + 2BC + CD. Наименьшее значение функция φ(x)принимает тогда, когда точка М совпадает с точкой В; это значение равно AB + 2BC + CD. 3) b < х < с; φ(x) при этих значениях х постоянна и равна AB + 2BC + CD. 4) с < х < d; наименьшее значение функция φ(x) принимает при х = с; оно равно также AB + 2BC + CD. 5) х > d; наименьшее значение функции φ(x) равно AB + 2BC + 3CD. Сравнивая полученные результаты, видим, что наименьшее значение функции φ(x) равно AB + 2BC + CD, или b — а + 2(с — b) + d — c = d + c — b — a. Это значение функция φ(x) принимает при условии, что b < х < с __________________________________________________ |
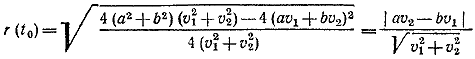
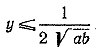 (6)
(6)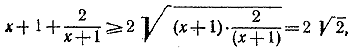 (1)
(1)