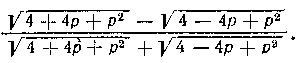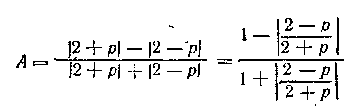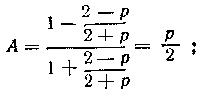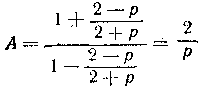ГЛАВА   2

АЛГЕБРАИЧЕСКИЕ   ПРЕОБРАЗОВАНИЯ

Предварительные   замечания

 При решении задач настоящей главы (начиная с задачи 72)  необходимо учесть следующее.

1.  Напомним,     что     корень  ⁿ√a    называется     арифметическим, если число а, из которого он извлекается, положительно  (или равно  нулю)   и если,  кроме того,  сам  корень берется  положительным.

Примеры. Выражение √— 27 не может представлять арифметического корня, так как подкоренное число отрицательно. Выражение ⁴√16 представляет арифметический корень, если рассматривать только положительное значение этого корня (т. е. 2). Выражение      ³√27 представляет арифметический корень (т. е. 3), если рассматривать  только   действительное  его   значение   (оно   имеет   еще два мнимых значения:    ) .

Выражение √— 16 не может представлять арифметического корня, так как под корнем отрицательное число.

2.  Излагаемые  в   алгебре   правила    преобразования   радикалов безоговорочно верны только для арифметических корней.

Например,    равенство  не верно при отрицательных значениях х.

Так, при х = —8 левая часть равенства имеет только одно действительное значение          ³√—8= — 2, а правая часть — два действительных значения ⁶√64  = ± 2 (если рассматривать и мнимые значения корней, то ³√—8 имеет три значения, a ⁶√64 —шесть).

Ввиду этого в настоящем разделе, где выполняются тождественные преобразования иррациональных выражений, мы принимаем, что все подкоренные выражения могут иметь только положительные (и нулевые) значения. Тем самым на буквенные величины, входящие в упрощаемые выражения, накладываются некоторые добавочные условия. В ряде случаев (см., например, замечания к задачам 75—81) мы указываем эти условия.

Иногда условия, которым должны удовлетворять буквенные величины, указываются в тексте задачи. Тогда при решении надо доказать, что при этих условиях все подкоренные выражения положительны.

3. Особо следует заметить, что равенство √x² = х (где √x² есть арифметический корень) верно только при х > 0.

При отрицательном же значении х оно не верно; вместо него имеет место равенство     √x² = — х.Оба случая можно объединить равенством √x² = |х|. Так, если х = —3, то     √(—3)² = √9 = —(—3) (при этом √(—3)² является арифметическим корнем, так как подкоренное число (—3)²  положительно и значение корня взято положительным). Можно также написать √(—3)² = | 3 |. Это замечание необходимо сделать потому, что его нет в большинстве учебников (в том числе и в «Алгебре» А. П. Киселева во всех многочисленных ее изданиях). Важность замечания видна из следующих примеров.

Пример  1. Упростить выражение

Решение  правильно только при т>п. При т<п вместо него нужно написать

т. е.

Так, если m =2 и n =3, то т — n = — 1, тогда как

Общая формула имеет вид

Пример 2. Упростить выражение

Обозначив для краткости данное выражение через А, имеем (при p =/= —2):

Если дробь     положительна, то

если же она отрицательна, то

Исследуем, при каких значениях р имеет место тот и другой случаи. Дробь  положительна, когда 2 — р и 2 + р   имеют   одинаковыe знаки. Потребуем сначала, чтобы величины 2 — р и 2 + р  были обе положительны. Величина 2— р положительна, когда    р < 2; величина 2 + р положительна, когда р > —2. Следовательно, обе величины 2 — р и 2 + р  положительны при —2< р <2. Потребовав же, чтобы величины 2 — р и 2 + р  были обе отрицательны, мы найдем, что это требование невыполнимо, так как 2 — р отрицательна при р >2, а 2 + р отрицательна при р <—2, а эти условия не совместны.

Значит, дробь положительна только    при    —2 < р < 2.    При значениях р>2, а также при значениях р <—2 дробь  отрицательна.

Таким образом, A = ^p/₂    при |р|<2     и    А = ²/_p   при   |р|>2.   При |р|=2 годятся оба выражения.

Пример 3. Равенство √a⁶ = а³ верно только при а > 0. При отрицательных значениях а вместо   него    имеет   место   равенствo  √a⁶ = — а³

Так, при а = — 1 имеем √(—1)⁶ =  — (—1) = +1. Здесь√(—1)⁶ есть арифметический корень, так как подкоренное число (—1)⁶=1 положительно, и значение корня взято положительным.

Пример 4. Вынести множители за знак радикала в выражении .

Данный корень может быть арифметическим только при а >3, так как при а<3 множитель (а—3)³, а вместе с ним и все подкоренное выражение отрицательны. Равенство

верно только при  а >5. При а<5   вместо   него   нужно   написать

Общая формула будет

4. Вообще равенство  ⁿ√x ⁿ  =  x (где левая часть обозначает арифметический корень) верно только для положительных значений х (и при х = 0). Если п —четное число, то при отрицательном значении х вместо  ⁿ√x ⁿ  =  x  имеем равенство  ⁿ√x ⁿ  = — x Если же п -  нечетное число, то при отрицательном значении х вовсе нет арифметического корня.