|
34. Пусть О1 и О2 —центры данных окружностей. Проводим прямую О1A и через центр О2 второй окружности прямую, параллельную О1A, которая пересекает вторую окружность в точках М и N (рис. 42).
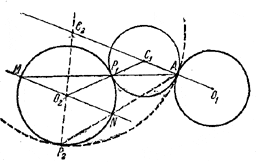
Рис.42.
Прямая МА пересечет вторую окружность в точке Р1. Прямая O2P1 пересечет О1A в точке С1.
Из подобия треугольников MO2P1 и АС1Р1 следует:
С1А = С1Р1.
Следовательно, окружность с центром С1 и радиусом С1А является искомой.
Второе решение получается с помощью точки N так же, как первое с помощью точки М. Если одна из прямых МА или NA будет касательной ко второй окружности, то останется одно решение, а второе даст эту касательную (центр окружности в бесконечности). Это будет тогда и только тогда, когда А совпадет с точкой касания одной из четырех общих касательных к данным окружностям.
________________________________________________
35. Пусть О — центр данной окружности, АВ — данная прямая (рис. 43).
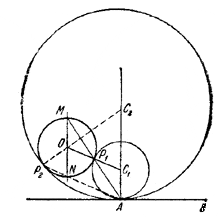
Рис.43.
Задача решается аналогично предыдущей. В общем случае она имеет два решения. Особыми случаями будут следующие:
1) данная прямая пересекает окружность, и данная точка А совпадает с одной из точек пересечения (нет ни одного решения);
2) данная прямая касается окружности, а точка А не совпадает с точкой касания (одно решение);
3) данная прямая касается окружности, и точка А совпадает с точкой касания (бесконечно много решений).
________________________________________________
36. Через центр О данной окружности проводим прямую, перпендикулярную к данной прямой l, пересекающую окружность в точках М и N (рис. 44).
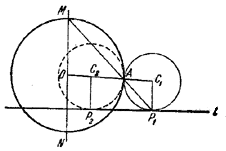
Рис.44.
Прямая МА пересечет l в точке P1 . Точка C1 есть точка пересечения перпендикуляра к l в точке Р1 и прямой ОА.
Из подобия треугольников АОМ и АС1 Р1 следует, что C1 A = C1 P1 .
Следовательно, окружность с центром С1 и радиусом С1 А является искомой.
Второе решение получается с помощью точки N так же, как первое с помощью точки М. Если прямая l не проходит через одну из точек А, М, N и точка А не совпадает с М или N, то задача всегда имеет два решения.
Пусть А не совпадает с М или N; если l проходит через М или через N, то задача имеет одно решение (вторая окружность совпадает с данной окружностью); если же l проходит через А, то задача не имеет ни одного решения.
Пусть А совпадает с М; если l не проходит через М или N, то задача имеет одно решение (второе переходит в прямую l ); если l проходит через N, то решением будет данная окружность, а если l проходит через М, то задача имеет бесконечно много решений.
________________________________________________
37. На данной гипотенузе АВ = с, как на диаметре, построим окружность с центром в точке О (рис. 45).
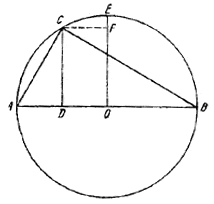
Рис.45.
Проведем OE_|_AB и на ОЕ отложим OF = h. Прямая, параллельная АВ и проходящая через F, пересечет окружность в искомой точке С. Задача разрешима, если h < c/2. Длины катетов а, b найдутся из системы уравнений
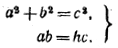
Решив эту систему, получим:
________________________________________________
38. Берем отрезок АВ и на прямой АВ от точки А в сторону В откладываем отрезок AE = AD (рис. 46).
Рис.46.
Строим /\ ВСЕ на основании BE со сторонами ВС и EC = CD. На отрезке АС, как на основании, строим /\ ACD со сторонами AD и CD.
Четырехугольник ABCD искомый, так как он имеет данные стороны и / DAC = / САЕ (треугольники ACD и АСЕ по построению равны).
________________________________________________
39. Пусть Н, S, М —точки пересечения высоты, биссектрисы и медианы соответственно с описанной окружностью К, имеющей центр O (рис. 47).
Рис.47.
Проведем прямую SO и через H — прямую, параллельную SO, которая второй раз пересечет K в точке А.
Проведем прямую AM, которая пересечет SO в точке Р.
Через Р проведем прямую, перпендикулярную к SO, которая пересечет окружность в точках В и С.
Треугольник ABC искомый, так как АН _|_ ВС, 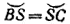 и ВР = РС. и ВР = РС.
Задача разрешима тогда и только тогда, когда Н, S, М не лежат на одной прямой, касательная к K в точке Н не параллельна SO, точки Н и М лежат по разные стороны от прямой SO, Но не на одном диаметре круга K.
________________________________________________
40. А. Случай внешнего касания. Из точки О пересечения биссектрис внутренних углов треугольника ABC опустим перпендикуляры ОМ, ON, OP на стороны треугольника (рис. 48).
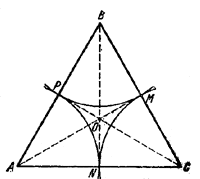
Рис.48.
Тогда АР = AN, BP = BM, CM = CN. Следовательно, окружности радиусов АР, ВМ, CN с центрами в А, В, С будут касаться друг друга в точках Р, М, N.
Б. Случай внутреннего касания. Из точки О пересечения биссектрисы угла С и биссектрис внешних углов А и В опустим перпендикуляры ОМ, ON и ОР на стороны (или на продолжения сторон) треугольника ABC (рис. 49).
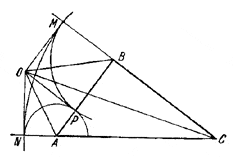
Рис.49.
Тогда AP = AN, BP = BM, CM = CN.
Следовательно, окружности радиусов АР, ВМ, CN с центрами А, В, С будут касаться друг друга в точках Р, М, N. Еще два решения получим, беря биссектрисы внутреннего угла А и внешних В и С или внутреннего угла В и внешних А и С.
________________________________________________
41. Решение основано на следующем свойстве: если высоты hA и hB вписанного треугольника ABC пересекают окружность в точках А1 и B1 , то вершина С делит дугу А1В1 пополам (рие. 50).
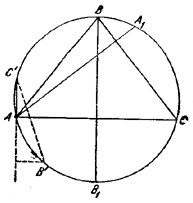
Рис.50.
Это следует из равенства углов / А1АС и / В1ВС, каждый из которых равен
π/2 — / ACB.
Построение.
Через А проводим прямую в данном направлении до пересечения с окружностью в точке А1 : пусть В1 — точка пересечения высоты hB с окружностью; находим середину С дуги А1В1 и проводим АС; проводим B1B _|_ AС; треугольник ABC искомый.
Второе решение АВ'С' получится, если взять середину С второй из дуг А1В1.
________________________________________________
42. Середину Е основания АВ соединим с вершиной С и найдем точку Q пересечения прямых ЕС и AD (рис. 51).
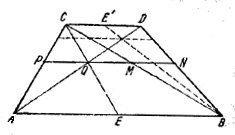
Рис.51.
Прямая PQMN, параллельная АВ,—искомая.
Действительно,
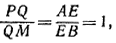
откуда PQ = QM; далее,
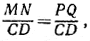
откуда MN = PQ. Второе решение получается с помощью середины Е' основания CD так же, как первое — с помощью Е.
________________________________________________
43. Пусть квадрат ABCD построен, причем В — заданная вершина, Е и F—данные точки (рис. 52).
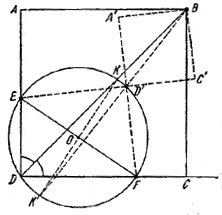
Рис.52.
Вершина D должна лежать на окружности, построенной на EF, как на диаметре. Пусть BD пересекает окружность в точке K. Тогда 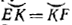 , так как / ADB = / BDC. , так как / ADB = / BDC.
Построение.
На EF, как на диаметре, построим окружность и из ее центра восставим перпендикуляр к EF до пересечения с окружностью в точках К и К'; соединим В с К и продолжим ВК до пересечения с окружностью в точке D; проведем прямые DE и DF и через точку В — перпендикулярные к ним В А и ВС. ABCD—искомый квадрат.
Второе решение получим, используя точку К'. Задача всегда имеет два решения, кроме того случая, когда точка В лежит на окружности с диаметром EF. В этом последнем случае задача решений не имеет, если точка В не совпадает с одной из точек К, К'.
________________________________________________
44. Первое решение. Проводим AD || MB до пересечения с продолжением ВС в точке D (рис. 53).
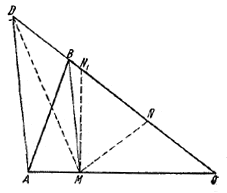
Рис.53.
На отрезке CD находим точку N такую, чтобы
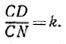
Прямая MN искомая, так как площадь SABM = SDBM следовательно, SABC = SDMC и по построению SDMC = kSNMC
Второе решение получим, используя точку N1 такую, что
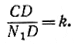
Тогда
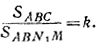
Учитывая возможность аналогичного построения, исходящего из вершины С (вместо А), легко убедиться в том, что при k =/= 2 задача всегда имеет два решения, а при k = 2—только одно.
________________________________________________
45. Для построения достаточно знать высоту h = KL прямоугольника.
Пусть прямоугольник KLMN искомый, KN лежит на АС (рис. 54).
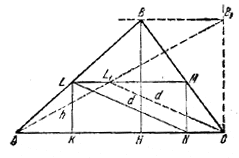
Рис.54.
Если перемещать вершину В параллельно основанию АС и сохранять при этом величину h неизменной, то будут сохраняться также величины основания и диагонали прямоугольника (ибо LM составляет ту же часть АС, какую составляет ВН — h от ВН). Значит, для нахождения h можно данный треугольник ABC заменить любым другим с тем же основанием АС и той же высотой ВН. Удобнее всего взять треугольник с прямым углом при основании.
Отсюда получаем следующее построение.
Проводим через В прямую, параллельную АС, а через С — прямую, перпендикулярную к АС; из вершины прямого угла С раствором циркуля, равным длине d данной диагонали, делаем засечку L1 на гипотенузе АВ1, через L1 проводим прямую параллельно АС; точки ее пересечения L и М со сторонами АВ и ВС являются вершинами искомого прямоугольника. Смотря по тому, будет ли высота треугольника АВ1С, опущенная из С, меньше, равна или больше данной величины d, задача будет иметь два решения, одно или ни одного.
________________________________________________
46. В данный угол впишем данную окружность. От точек касания А и В на сторонах угла отложим по направлению от вершины отрезки АС и BD, равные данной стороне треугольника (рис. 55).
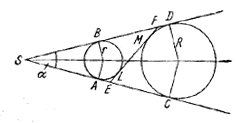
Рис.55.
Впишем в данный угол вторую окружность так, чтобы она касалась сторон угла в точках С и D. Проведем общую касательную EF к построенным окружностям. Докажем, что полученный таким образом /\ SEF есть искомый. Для этого достаточно доказать, что AC = FE. Нетрудно убедиться в том, что периметр /\ SEF равен 2SC; с другой стороны, он, очевидно, равен 2 (SA + EL + LF).
Итак, SC = SA + EL + LF, SA + AC = SA + EF, т.е.
AC = EF,
что и требовалось доказать.
Ясно, что задача имеет два решения, если окружности не пересекаются, и одно, — еcли они касаются. Задача не разрешима, если окружности пересекаются.
Пусть α — данный угол, r и R — радиусы окружностей, а — данная сторона треугольника.
Расстояние мeжду центрами окружностей равно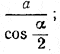 для разрешимости задачи требуется, чтобы для разрешимости задачи требуется, чтобы
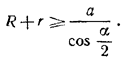
Но
R = r + a tg α/2
и, следовательно, должно быть
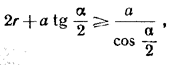
или
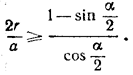
________________________________________________
47. Проводим окружность с центром в точке В, касающуюся прямой CD (рис. 56).
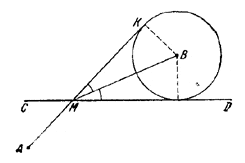
Рис.56.
Из точки А (если А и В лежат по разные стороны от CD, или из точки А', симметричной с А относительно CD, если А и В лежат по одну сторону от CD) проводим касательную АК к построенной окружности. Точка М, в которой АК (или А'К) пересечет CD, и есть искомая. Действительно,
/ AMC = / KMD = 2 / BMD.
________________________________________________
|