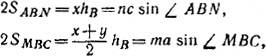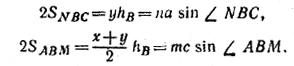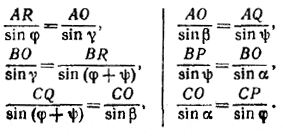ГЛАВА   3

ПЛАНИМЕТРИЯ

ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО

Ответы и решения

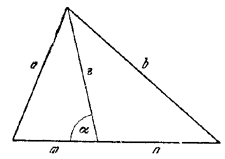
62. Пусть z — длина биссектрисы, т, п —длины отрезков, на которые она делит основание треугольника (рис. 68).

Pис. 68.

По теореме косинусов

а² = z² + т² — 2mz cos α,

b² = z² + n² + 2nz cosα.

Умножив первое   из  этих   равенств   на   п , второе  на  т и сложив, получим:

па² + тb²  = (т + п)(z²  + тп).                           (1)

В силу соотношения  ^a/_m = ^b/_n имеем:

Подставив это выражение в (1), получим требуемое равенство

ab = z²  + тп.

В случае а = b, т = п доказанное равенство выражает теорему Пифагора: а² = z² + т² .

________________________________________________

63. По условию   BD = EC   (рис. 69).  

Pис. 69

 Если   М —точка   пересечения ВС и DE, то из  /\  BDM и  /\  ЕСМ имеем:

________________________________________________

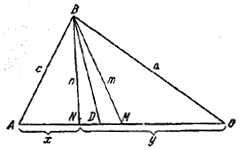
64. Пусть   BD, BE и BF суть соответственно высота, биссектриса и медиана в
/\  ABC. Предположим, что АВ < ВС.

Тогда

/  A > /  C,   /  CBD  > /  ABD,

откуда

/  CBD > ¹/₂ ( /  ABD + /  CBD) = ¹/₂ /  В,

т. е. /   CBD > /   СВЕ. Значит,   биссектриса   BE   проходит  внутри  /  CBD и точка Е лежит между D и С.

Далее,   ^AE/_EC = ^AB/_BC < 1, AE < EC, откуда

AE < ¹/₂ (AE + EC) = ¹/₂ AC,

т. e. AE < AF. Значит,  точка F лежит между E и С. Таким образом,  точка   Е    лежит между D   и  F,   что и требовалось доказать.

________________________________________________

65. В треугольнике ABC пусть BD— биссектриса, ВМ — медиана и BN — прямая, симметричная с ВМ относительно BD (рис. 70).

Pис. 70

Если S_ABN  и S_MBC — площади соответствующих треугольников, то

где h_B— высота, опущенная из вершины В на АС.

Так как /  ABN = /  МВС, то отсюда

                  (1)

Аналогично

Так как /   NВС = /   ABM, то отсюда

                    (2)

Поделив почленно (1) и (2), получим:

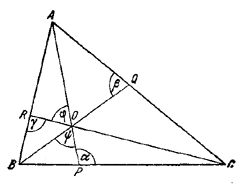
что и требовалось доказать.

________________________________________________

66.  Прямые АР, BQ и CR разбивают треугольник ABC на шесть треугольников:
/\ AOR, /\ROB, /\ВОР, /\РОС, /\COQ, /\QOA (рис. 71).

Pис. 71

Применяя теорему синусов к каждому из них, получаем:

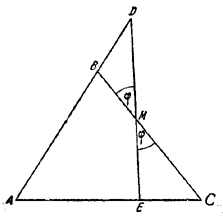
Перемножив почленно все эти равенства, находим: AR•BP•CQ = BR•AQ•CP.

________________________________________________

67. Пусть К и О — центры   описанного и вписанного в /\ AВС кругов   и   D —середина  дуги   АС  (рис. 72).   

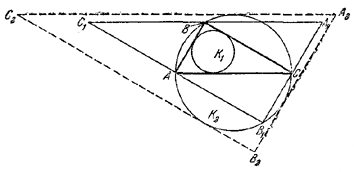
Pис. 72

Каждый из углов,  /  ОАD и / AOD, равен половине суммы углов при вершинах А и В треугольника ABC. Отсюда следует, что OD = AD.

По  теореме   о    хордах,   пересекающихся    внутри   круга,   имеем

MO•ON = BO•OD.

Далее, если ОЕ _]_ АВ и FD—диаметр, то треугольники ВОЕ и FDA подобны, откуда   ВО : ОЕ = FD : AD, так что BO•AD = OE•FD или, так как AD = OD, BO•OD = OE•FD.  Следовательно,

MO•ON = OE•FD.

Подставив в это равенство значения МО =  R + l, ON = R—  l, OE = r, FD = 2R, получим R² — l² =  2Rr , что и требовалось доказать.

________________________________________________

68.  Первое решение. Пусть ABC—данный треугольник, K₁ — вписанная окружность радиуса   r  и  K₂ — описанная окружность радиуса R. Построим вспомогательный треугольник A₁B₁C₁ так, чтобы его стороны были параллельны сторонам /\  ABC и проходили через вершины /\  ABC (рис. 73).

Pис. 73

Проведем касательные к окружности K₂, параллельные сторонам /\  A₁B₁C₁,  руководствуясь следующим правилом: касательная А₂В₂, параллельная стороне А₁В₁, касается K₂  в точке, лежащей на той же дуге , на которой лежит вершина С и т. д. Отрезки проведенных касательных образуют /\  A₂B₂C₂.

Тогда /\  A₁B₁C₁ лежит внутри /\  A₂B₂C₂ и эти два треугольника подобны. Поэтому радиус R' окружности, вписанной в /\  A₁B₁C₁, не больше радиуса R окружности K₂, вписанной в /\  A₂B₂C₂, т. е. R' < R;    с   другой    стороны,    отношение    радиусов   окружностей, вписанных в подобные треугольники A₁B₁C₁ и AВС, равно отношению сходственных   сторон   этих  треугольников,   т.   е. .   

Таким образом, R' = 2r. Сопоставляя это равенство с неравенством R' < R, окончательно получаем:

2r < R.

Второе решение. Пусть r, R —радиусы вписанной и описанной окружностей, S — площадь данного треугольника, р —полупериметр, а, b —стороны. Тогда

Но

Следовательно,

Задача сводится к доказательству неравенства

(см. задачу 256 Тригонометрические неравенства).

Третье решение. Из формулы  l² = R² — 2Rr, доказанной в предыдущей   задаче,   следует,   что   R² — 2Rr  > 0,   откуда  R  >  2r.

________________________________________________

69.  Пусть a, b —длины катетов и с—длина гипотенузы. Сравнив два выражения для площади треугольника, получаем:

S = ¹/₂ ( a + b + c ) r = ¹/₂ hc

откуда

Так как а + b > с, то

Далее, неравенство  a² + b² > 2ab в силу соотношения  c² = a² + b² равносильно неравенству 2c² >  (a + b)²,   или a + b < с √2.   Поэтому

________________________________________________

70.  Пусть   А, В, С —  углы треугольника,    а, b, с — противолежащие им стороны и  Р = a + b + c . Требуемое соотношение следует из равенств

ak_a +  bk_b + ck_c = Pr ,                                    (1)

(b + c)k_a + (c + a)k_b + (a  + b)k_c = PR,                    (2)

сложив которые, получим

k_a +  k_b + k_c = r + R.

Равенство (1) верно в силу того, что его левая и правая части равны удвоенной площади треугольника. Для доказательства (2) заметим,  что

k_a = R cos A,    k_b = R cos B,    k_c= R cos C               (3)

и что

b cos С+ с cos В  = a,
с cos A + a cos С = b,
a cos В+ b cos A = с,

откуда   почленным  сложением получим равенство

(b + c) cos A + (с + а) cos B + (a + b) cos C = P

которое   после   умножения   на  R и использования (3) совпадает с (2).

________________________________________________

71. Пусть A₂В₂,   B₂С₂,   С₂A₂— средние линии в  /\АВС,      А₃, В₃, С₃ — середины отрезков   АА₁ ,  ВВ₁ ,   СС₁  (рис. 74).

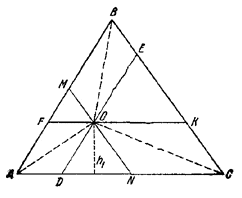
Pис. 74

Точки А₃, В₃, С₃  лежат на средних линиях /\АВС и притом не на концах этих линий, так как в противном случае по крайней мере одна из точек A₁ , B₁  , С₁ совпала бы с вершиной /\АВС.

Так как всякая прямая, не проходящая через вершины треугольника A₂В₂С₂, не пересекает одновременно все три его стороны, то точки  А₃, В₃, С₃  не лежат на одной прямой.

________________________________________________

72.  Если h₁ —высота   /\ DON, h_B—высота /\ ABC, a S_АОC и S_ABC — площади соответствующих треугольников, то (рис. 75)

Pис. 75

Сложив эти равенства, получим:

________________________________________________

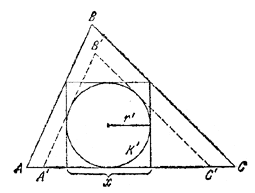
73.  Рассмотрим   окружность    К'   радиуса   r',   вписанную в  квадрат,   и   проведем   к  ней   касательные   А' В' | | АВ,   В'С' | | ВС (рис. 76).

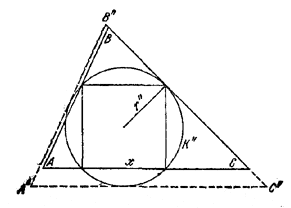
Pис. 76

Ясно, что /\ А'В'С' лежит внутри /\ ABC, и поэтому А'С' < АС.

Так как

/\ А'В'С' ~ /\ ABC,

то    откуда   х =  2r' < 2r.

2) Рассмотрим окружность К" радиуса r", описанную около квадрата, и проведем к ней касательные А"В" | | АВ, В"С'' | | ВС и А"C'' | | АС (рис. 77).

Pис. 77

Ясно, что /\ ABC лежит     внутри  /\ А"В"С"     и    поэтому      А"С'' > АС.      Так     как

/\ А"В"С'' ~ /\ ABC,

то , откуда      x = √2r" > √2r.

________________________________________________

74. Пусть в  /\ ABC  точка  М   есть  точка   пересечения   высот АА₁ ,  ВВ₁ ,  СС₁; Р — центр описанного круга радиуса R; С₂, А₂, В₂— середины  сторон   АВ,   ВС,   AC;       ОМ = ОР; ON_|_AC ;  A₃, В₃, С₃ — середины AM,  ВМ,  СМ (рис. 78).

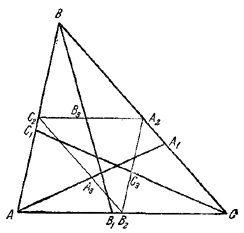
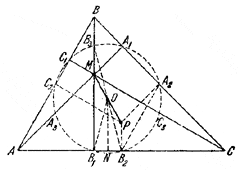
Pис. 78

Докажем, что точка О находится на равном расстоянии от А_i , В_i , С_i , где i = 1, 2, 3. Так как  ON — средняя   линия   в  трапеции   МВ₁В₂Р,   то   OB₁ = OB₂.   Из   подобия треугольников     АМВ    и    РА₂В₂    находим     ВМ =2РВ₂,    поэтому B₃M = PB₂.   Из   параллелограмма  МВ₃РВ₂ имеем ОВ₃ = ОВ₂. Но

ОВ₃ = ¹/₂ BP = ^R/₂

(как средняя   линия в треугольнике  РМВ). Следовательно,

ОВ₂ = ОВ₂ = ОВ₁ = ^R/₂.

Точно  так   же  доказывается,   что ОА₁ = ОА₂ = OА₃ = ОС₁ = ОC₂ = ОC₃ = ^R/₂

________________________________________________

75. В  /\ АВС пусть АА₁ ,  ВВ₁ ,  СС₁ —высоты, пересекающиеся в  точке   О,  
  C₁M | | B₁N _|_BC,    A₁P | | C₁Q _|_ AC,   В₁R | | A₁S _|_ АВ (рис.  79).

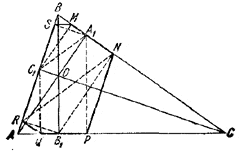
Pис.  79

1) Докажем, что SM  | |  АС.   Имеем   /\ ВА₁А ~ /\BC₁C как прямоугольные треугольники с общим острым углом ABC. Поэтому

Следовательно, /\А₁BC₁ ~ /\ ABC и /  ВА₁С₁ = /  ВАС. В /\  А₁ВС₁ отрезки A₁S и С₁М — высоты. Поэтому, повторив предыдущее рассуждение, покажем, что /  BSM = / BA₁C₁. Следовательно, /  BSM = /  ВАС и SM | | AС. Аналогично доказывается, что PN | | АВ и RQ | | BC.

2) Для доказательства того, что вершины шестиугольника MNPQRS лежат на одной окружности, достаточно доказать, что любые четыре его последовательные вершины лежат на одной окружности. Это следует из того, что через три   точки, не лежащие на одной прямой, можно провести только одну окружность. Имеются четверки последовательных вершин рассматриваемого шестиугольника двух типов: такие, в которых средние точки лежат на разных сторонах /\ ABC (RSMN, MNPQ, PQRS), и такие, в которых средние точки лежат на одной стороне /\ ABC (NPQR, QRSM, SMNP).

Рассмотрим четверки RSMN и NPQR (разных типов). Из очевидной пропорциональности

следует, что NR | | A₁C₁ Поэтому

/  MNR = /  BA₁C₁ = /  ВАС = /  BSM.

Значит, /  MNR + /  MSR = π и точки R, S, М, N лежат на одной окружности. Далее,

/  PNR + /  PQR = π — ( /  PNC + /  BNR) + π — /  AQR =
= 2π — ( /  AВС+ /  ВАС+ /  AСВ) = π,

откуда следует, что точки N, P, Q, R также лежат на одной окружности. Аналогично проводится доказательство для остальных четверок.

________________________________________________