|
76. Пусть А1 , B1 , C1 — точки касания вписанного круга со сторонами /\ ABC, D — центр вписанного круга (рис. 80).
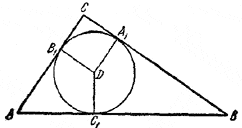
Pис. 80
Так как отрезки касательных, проведенных из одной точки к окружности, равны, то
СА1 = СВ1, ВА1 = ВС1, АВ1 = АС1.
Кроме того,
DB1 = CA1 , B1C = A1D.
Следовательно,
АС + ВС = СА1 + А1В + CB1 + B1A = B1D + A1D + BC1 + AC1 = 2r + 2R,
где r —радиус вписанного, а R —радиус описанного круга.
________________________________________________
77. Пусть в /\ ABC угол ABC прямой, BD—высота, BE—биссектриса и BF — медиана (рис. 81).
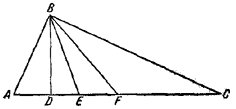
Pис. 81
Так как BF = FC, то / CBF = / AСВ. Но
/ ABD = π/2 — / BAD = / АСВ .
Следовательно, / ABD = / СВР и
/ DBE = / ABE — / ABD = / CBE — / CBF = / FBE,
что и требовалось доказать.
________________________________________________
78. Симметрия в расположении ABC и A1B1C1 относительно центра вписанного круга О означает, что соответствующие точки /\ ABC и /\ А1В1С1 лежат на одной прямой с О и находятся на равном расстоянии от О (рис. 82).
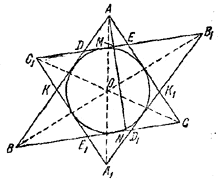
Pис. 82
В частности, ОС = ОС1, ОВ = ОВ1 и ВСВ1С1—параллелограмм; значит, ВС = В1С1. Аналогично АС = А1С1, АВ = A1B1 и /\ ABC = /\ А1В1С1. Рассматривая параллелограммы АВА1В1, BDB1D1, ACA1C1 и ECE1C1, находим, что AD = A1D1 , АЕ = А1Е1, а так как / A = / А1 то /\ ADE = /\ A1D1E1. Аналогично /\ B1EK1 = /\ BE1K и /\ DС1K = /\ D1СK1
Введем обозначения:
S—площадь /\ ABC,
S1—площадь /\ ADE,
S2—площадь /\ DC1K,
S3—площадь /\ KВЕ1,
АВ = с, ВС = а, АС = b,
hA, hB, hC — высоты, опущенные из вершин А, В, С. Тогда
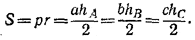
Пусть AM—высота в /\ ADE, AN—высота в /\ ABC; тогда
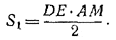
Из подобия треугольников ABC и ADE находим:
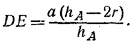
Следовательно,
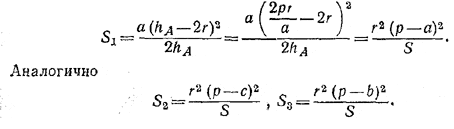
Используя формулу Герона, получаем:
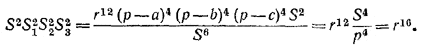
________________________________________________
79. В обозначениях рис. 83 имеем:
МА2 = МO2 + АO2 — 2МO•АО cos α,
МС2 = МО2 + СО2 + 2МО•СО cos α.
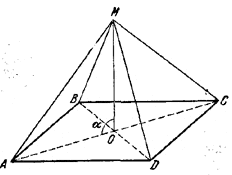
Pис. 83
Так как AО = СО, то, сложив эти равенства, получим;
МА2 + МС2 = 2МО2 + 2АO2. (1)
Аналогично
MB2 + MD2 = 2MO2 + 2BO2.
Следовательно, разность
(МА2 + МС2) — (МВ2 + MD2) = 2(AО2 — ВО2)
не зависит от положения точки М.
________________________________________________
80. Пусть О — точка пересечения прямых AA1 и СС1 ( рис. 84).
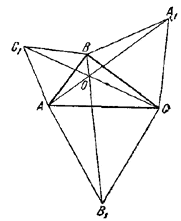
Pис. 84
Задача будет решена, если будет доказано, что
/ АОВ + / АОВ1 = 180°. (1)
Заметим, что /\ С1ВС = /\ ABA1, так как
С1B= АВ, ВС = ВА1 и / С1ВС = 60° + / AВС = / ABA1
Поэтому / ОС1В = / ОАВ и четырехугольник ОАС1В вписан в некоторую окружность. Следовательно, / АОВ = 120°. Аналогично покажем, что / ВОС= 120°.
Но тогда и / AОС= 120, откуда следует, что четырехугольник АОСВ1 вписан в некоторую окружность. Но отсюда следует, что / АОВ1= / АСВ1 = 60°. Поэтому (1) верно.
________________________________________________
81. В обозначениях рис. 85 имеем:
/ PBR = / ABC
и
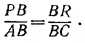
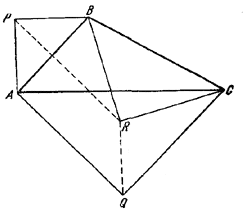
Pис. 85
Поэтому /\ PBR ~ /\ ABC и аналогично /\ QRC ~ /\ ABC. Пользуясь этим, получим:
/ APR = / APB — / BPR = / APB — / BAC,
поэтому
/ APR + / PAQ = / APB + 2 / РАВ = π,
так что PR | | AQ. Аналогично докажем, что QR | | АР.
________________________________________________
82. Обозначим через hB, hC и hD расстояния от вершин В, С и D параллелограмма до прямой АО (рис. 86).
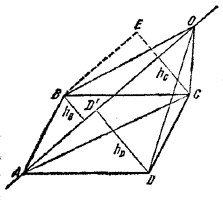
Pис. 86
Тогда имеет место следующее свойство: наибольшее из этих трех расстояний равно сумме двух других. Например, если АО пересекает сторону ВС (как на рис. 86), то, проведя BE | | АО и CE_|_AO, из равенства треугольников ВЕС и AD'D найдем:
hD = hB + hC
Аналогично, если АО пересекает сторону CD то hB = hC + hD, если АО не пересекает сторон ВС и CD, то hC = hB + hD. Из этого свойства для случая, показанного на рис. 86, сразу следует равенство для площадей треугольников:
SAOC = SAOD — SAOB
Вообще, очевидно, можно написать формулу
SAOC = | SAOD ± SAOB |
где берется знак плюс, если точки В и D лежат по одну сторону от АО, и знак минус, если точки В и D лежат по разные стороны от АО.
Повторение этого рассуждения для прямой СО вместо АО приводит к аналогичной формуле
SAOC = | SCOD ± SCOB |
с тем же правилом выбора знаков, но относительно прямой СО.
________________________________________________
83. Достроим трапецию ABCD до треугольника AMD и соединим M c серединой F основания AD (рис. 87).
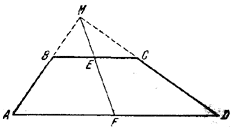
Pис. 87
Тогда
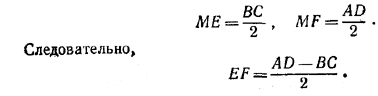
________________________________________________
84. Пусть ABCD — данная трапеция с основаниями AD и ВС и пусть BE _|_AD, CF _|_ AD (рис. 88).
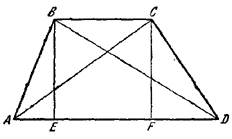
Pис. 88
Имеем:
AC2—AF2= CD2 — FD2,
BD2 — ED2 = AB2 — AE2.
Сложив эти равенства, получим:
АС2 + BD2 = AВ2 + CD2 + AF2 — FD2 + ED2 — AE2 =
= AВ2 + СD2 + AD(AF — FD + ED — AE)=
= AВ2 + CD2 + AD • 2EF = AВ2 + CD2 + 2AD • ВС.
________________________________________________
85. Пусть дана трапеция ABCD с параллельными основаниями AD и ВС, E — середина ВС, F—середина AD и О—точка пересечения диагоналей (рис. 89).
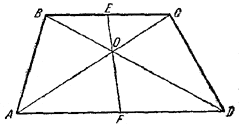
Pис. 89
Треугольники AOF и СОЕ подобны (это следует из подобия треугольников AOD и СОВ). Поэтому / AOF = / СОЕ, т. е. EOF—прямая.
________________________________________________
86. Пусть ABCD—данный четырехугольник и точки М, N являются серединами сторон, соответственно, АВ и CD ( рис. 90).
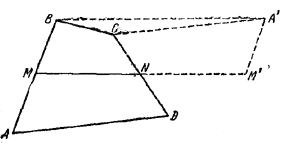
Pис. 90
Повернем четырехугольник AMND в плоскости рисунка вокруг вершины N на 180°. Тогда вершина D совпадает с С, а вершины М, А займут положение M', А'. При этом точки М, N, М' расположатся на одной прямой и, кроме того, будет М'А' | | MB и М'А' = MB. Поэтому МВА'М'— параллелограмм и A'B = M'M=2MN. Так как, по условию BC+AD = 2MN, то ВС + СA' = A'В. Следовательно, точка С лежит на отрезке А'В: в противном случае в /\ ВСA' мы имели бы ВС + СА' > А'В. Отсюда следует, что ВС | | MN | | AD, т. е. ABCD — трапеция.
________________________________________________
87. Найдем выражение для площади четырехугольника через диагонали и угол между диагоналями. Пусть О — точка пересечения диагоналей четырехугольника ABCD и / ВОА= α (рис. 91).
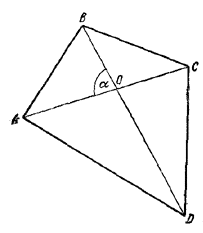
Pис. 91
Тогда площадь данного четырехугольника равна
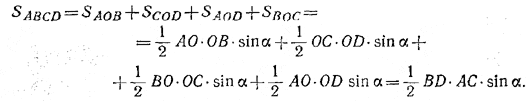
Из этой формулы и следует справедливость доказываемого утверждения.
________________________________________________
88. Пусть М—внутренняя точка выпуклого многоугольника, а АВ—его сторона, наименее удаленная от М. Докажем, что основание перпендикуляра Р, опущенного из М на АВ, лежит на АВ, а не на ее продолжении (рис. 92).
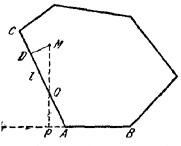
Pис. 92
Действительно, если Р лежит вне АВ, то МР пересечет некоторую сторону l многоугольника в точке Q, причем, в силу выпуклости многоугольника, MQ < МР. Но расстояние DM от М до l меньше MQ, а значит и меньше МР, что противоречит выбору стороны АВ.
________________________________________________
89. Пусть АА1 , ВВ1 , CC1 , DD1 — биссектрисы внутренних углов параллелограмма ABCD, образующие в пересечении четырехугольник PQRS (рис. 93).
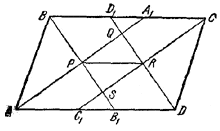
Pис. 93
Очевидно, ВВ1 | | DD1 и АА1 | | СС1. Кроме того,
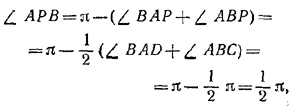
так что PQRS — прямоугольник. Треугольники ВАВ1 и CDC1 — равнобедренные, так как в них биссектрисы перпендикулярны основаниям. Поэтому ВР = РВ1, D1R = RD и, следовательно, PR | | AD.
Таким образом, PRDB1 — параллелограмм и
PR = B1D = AD — AB1 = AD — AB.
________________________________________________
|