|
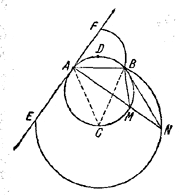
118. Искомое геометрическое место состоит из двух дуг окружностей: дуги BE с центром в середине С дуги АВ данной окружности и дуги BF с центром в середине второй дуги АВ данной окружности, причем EAF—касательная в точке А к данной окружности (рис. 123).
Pис. 123
Доказательство. Пусть N — точка искомого геометрического места, полученная с помощью точки М, взятой на нижней дуге АВ. По построению /\ NMВ равнобедренный, откуда
/ BNA =1/2 / BMA = 1/2 / ВСА.
Следовательно, точка N лежит на окружности с центром С, проходящей через точки А и В. Далее, точка N должна находиться внутри / ВАЕ, т. е. она лежит на дуге BE окружности с центром С. Обратно, если N лежит на этой дуге, то
/ BNA = 1/2 / ВСА= 1/2 / ВМА,
откуда следует, что / BNA= / NBM и /\ NMB равнобедренный. Значит, точка N получается указанным построением. Аналогично проводится доказательство в случае, когда точка М будет на верхней дуге АВ.
________________________________________________
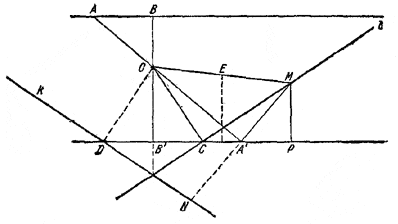
119. Искомое геометрическое место состоит из двух прямых l и k, симметрично расположенных относительно общего перпендикуляра ВВ' к данным параллельным прямым, проведенного через точку О. Прямая l проходит через точку С перпендикулярно к ОС, причем В'С = ОВ (рис. 124).
Pис. 124
Доказательство. Пусть М и N — точки, полученные при построении с помощью секущей А А'. Доказательство проведем только для точки М (для N оно проводится аналогично).
Пусть MР_|_В'С; тогда / ОАВ = / А'МР (как углы с перпендикулярными сторонами). Поэтому прямоугольные треугольники ОАВ и А'МР, имеющие равные гипотенузы ОА и А'М, равны. Значит, А'Р = ОВ = В'С. Отсюда следует, что если Е — середина ОМ, то точки М, А', С, О лежат на одной окружности с центром E и, следовательно, МС_|_ ОС, т. е. точка М лежит на прямой l . Обратно, если М—какая-нибудь точка прямой l и / МА'О прямой, то А'Р = В'С = ОВ, откуда следует равенство треугольников ОАВ и А'МР и, наконец, равенство ОА = А'М. Следовательно, точка М получается рассматриваемым построением.
________________________________________________
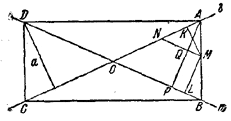
120. В случае пересекающихся прямых искомое геометрическое место состоит из четырех отрезков, образующих прямоугольник ABCD, вершины которого лежат на данных прямых l , m и находятся от них на данном расстоянии а (рис. 125).
Pис. 125
Доказательство. Пусть точка М такова, что МК _|_ l, ML_|_m и MK + ML = a, где а —длина данного отрезка.
Проведем через М прямую АВ так, чтобы ОА = ОВ и MN | | ОВ. Пусть АР_|_ОВ и Q— точка пересечения АР и MN. Из равенства AN = MN следует, что MK = AQ и, значит,
AP = AQ + QP = MK + ML = a.
Следовательно, точка А является вершиной упомянутого прямоугольника. То же верно и для точки В, так что М лежит на стороне этого прямоугольника. Обратно, если М лежит на стороне этого прямоугольника, то, проведя рассуждение в обратном порядке, получим, что MK+ ML = AP = a.
Если данные прямые l и m параллельны и расстояние между ними равно h, то искомое геометрическое место существует только тогда, когда a > h, и представляет собой пару прямых, параллельных данным, при а > h или всю полосу между l и m при a = h.
________________________________________________
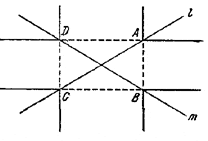
121. В случае пересекающихся прямых искомое геометрическое место состоит из восьми полупрямых, являющихся продолжениями сторон прямоугольника ABCD, указанного в решении задачи 120 (рис. 126).
Pис. 126
Доказательство аналогично тому, которое дано в решении этой задачи.
Если данные прямые l и m параллельны и расстояние между ними равно h, то искомое геометрическое место существует только тогда, когда a < h, и представляет собой пару прямых, параллельных данным, при а < h или часть плоскости, лежащую вне полосы между l и m, при a = h.
________________________________________________
122. Если отрезок АВ лежит на прямой l , a CD—на прямой т, то искомое геометрическое место состоит из четырех отрезков, образующих параллелограмм PQRS, в котором l и m —диагонали, а положение вершин Р и Q определяется из соотношений
hPCD = a2, hQ AB = a2, (1)
где hP и hQ — расстояния точек Р и Q от прямых m и l (рис. 127).
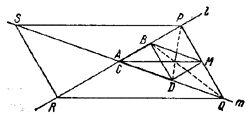
Pис. 127
Доказательство. Заметим, что при фиксированных l и m искомое геометрическое место вполне определяется заданием длин отрезков АВ и CD и постоянной а, но не зависит от положения этих отрезков на прямых l и m. Действительно, при изменении этого положения площади треугольников АМВ и CMD не меняются. Поэтому достаточно рaссмотреть частный случай, когда отрезки АВ и CD имеют общий конец в точке пересечения прямых l и m. В этом случае отрезки АВ и CD будут сторонами треугольника, третья сторона которого лежит в одном из четырех углов, образующихся при пересечении прямых l и m. Например, на рис. 127 совмещены концы А и С и третьей стороной является BD.
Пусть М—точка искомого геометрического места, лежащая внутри угла BAD. Тогда площадь /\ BMD равна
SBMD = | SAMB + SCMD — SABD | = | a2 — SABD |
Отсюда следует, что расстояние точки М от прямой BD не зависит от ее положения на прямой PQ || BD. Для точек Р | | Q выполнены соотношения (1).
Обратно, пусть М — какая-нибудь точка на прямой PQ, где точки Р и Q построены согласно (1). Из соотношений
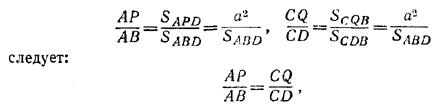
т. е. PQ || BD. Поэтому
SAMB + SCMD = SABD+ SBMD = SABD+ SBPD = SAPD = a2
Следовательно, точка М принадлежит искомому геометрическому месту. Остальные стороны параллелограмма PQRS получаются аналогично при совмещении других концов отрезков, а именно: QR при В = С, RS при В = D и SP при A = D.
________________________________________________
123. Искомым геометрическим местом является окружность, симметричная с данной окружностью К относительно данной хорды АВ (рис. 128).
Pис. 128
Доказательство. Построим в окружности К хорду AD_|_ AB. Пусть /\ ABC вписан в К и М — точка пересечения его высот. Легко видеть, что AMCD — параллелограмм: DA| | СМ как перпендикуляры к АВ, a DC | | AM как перпендикуляры к ВС (DC_|_BC, так как BD — диаметр в К). Поэтому точка М лежит на окружности К', получаемой из окружности К сдвигом на расстояние AD в направлении хорды DA. Ясно, что эта окружность K' симметрична с К относительно АВ.
Обратно, пусть М—точка на К' и МС_|_АВ. Так как MC = AD, то AMCD — параллелограмм и, значит, АМ | | DC. Но DC _|_ ВС, так как ABCD вписан в К и угол BAD прямой. Поэтому AM _|_ ВС и М—точка пересечения высот в /\ ABC. Следовательно, М принадлежит искомому геометрическому месту.
________________________________________________
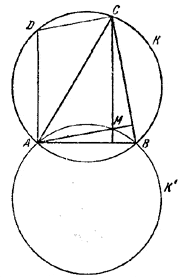
124. Пусть О — центр и R — радиус данной окружности (рис. 129).
Pис. 129
Искомым геометрическим местом является прямая l , перпендикулярная к прямой ОА и пересекающая эту прямую в точке В такой, что
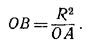 (1) (1)
Доказательство. Проведем через точку М прямую l_|_ ОA, которая пересечет прямую ОА в точке В. Пусть С — точка пересечения отрезка ОМ с хордой KL. Из подобия треугольников ОАС и OMB следует:
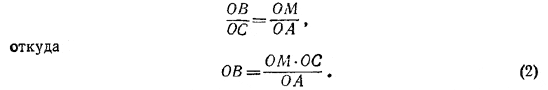
По построению КС есть высота в прямоугольном треугольнике ОКМ, следовательно,
ОМ•ОС = R2.
Подставив это выражение в (2), получим равенство (1).
Обратно, пусть М — какая-нибудь точка прямой l, перпендикулярной к ОА и такой, что ОВ определяется равенством (1). Проведем касательную МК и КС_|_OМ. Пусть КС пересечет прямую ОА в точке А'. Тогда, повторив первую часть доказательства, найдем, что ОВ определяется формулой (1) с ОА' вместо ОА. Отсюда получим ОА' = ОА, т. е. точка А' совпадет с A, а это означает, что точка М принадлежит искомому геометрическому месту.
________________________________________________
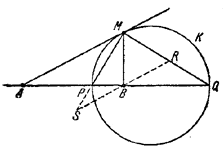
125. Пусть
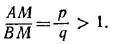
Проведем биссектрисы МР и MQ двух смежных углов с вершиной М и сторонами МА и MB (рис. 130).
Pис. 130
Тогда по свойству биссектрис будем иметь:
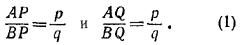
Отсюда следует, что положение точек Р и Q не зависит от положения точки М. Так как, кроме того, / PMQ = π/2 , то точка М лежит на окружности К с диаметром PQ. Обратно, пусть точки Р и Q построены согласно (1) и К—окружность с диаметром PQ. Если точка М лежит на этой окружности, то / PMQ = π/2 .
Через точку В проведем RS | |AM, тогда
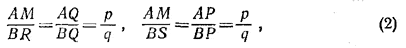
откуда BR = BS и ВМ — медиана в /\ RMS. Так как /\ RMS — прямоугольный, то BM=BR и в силу (2)
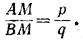
Поэтому точка М принадлежит рассматриваемому геометрическому месту.
Чтобы выразить диаметр PQ через длину а отрезка АВ из соотношений
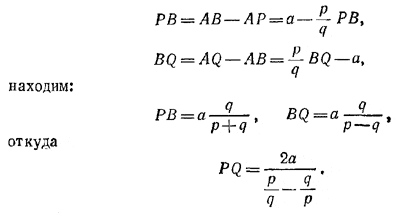
Если p = q, то искомым геометрическим местом будет, очевидно, перпендикуляр к прямой АВ, проведенный через середину отрезка АВ.
________________________________________________
126. Искомое геометрическое место есть перпендикуляр к отрезку АВ, проведенный через его середину Е, с выброшенной точкой Е.
Доказательство. Треугольник ADB — равнобедренный, так как / CAD = / CBD, ибо эти углы опираются в равных окружностях на равные дуги CD (рис. 131).
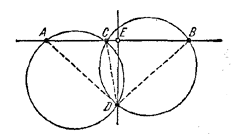
Pис. 131
Поэтому точка D лежит на перпендикуляре к отрезку АВ, проведенному через его середину Е. Наоборот, если взять любую точку D на этом перпендикуляре, не совпадающую с точкой Е, то окружности, проходящие через ACD и BCD, равны. Это следует, например, из равенств
где α = / BAD и β = / CBD.
________________________________________________
127. Искомое геометрическое место есть прямая, проведенная через какие-нибудь два различных положения последней вершины.
Доказательство. Пусть, например, A1В1С1D1E1 — одно и A2В2С2D2E2 — другое положения деформирующегося многоугольника, вершины А, В, С, D которого скользят соответственно по прямым lA, lB, lC, lD, (рис. 132).
Pис. 132
Через положения Е1 и E2 последней вершины проведем прямую l . Пусть вершина на прямой lA заняла положение А, а на lD — соответствующее положение D. Сторона, параллельная A2E2, пересечет l в точке E', а сторона, параллельная D2E2 ,— в точке Е". По построению
откуда
E'E2 = E''E2
т. е. точки E' и E" совпадают. Это означает, что последняя вершина будет лежать на прямой l в точке Е = Е' = E''.
Обратное очевидно, так как положение деформированного многоугольника можно построить, начиная с любой точки Е на прямой l.
________________________________________________
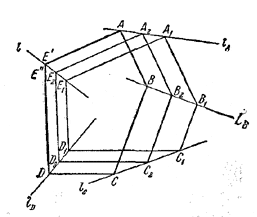
128. Искомое геометрическое место есть окружность, проходящая через концы хорды АВ и одну из точек M1, получаемых указанным в условии построением.
Доказательство. Предварительно введем некоторые обозначения. Найдется одно и только одно такое положение C1D1 хорды CD, когда C1D1 | | AB и когда на данной окружности К можно выбрать такое направление обхода v, при движении в котором концы хорд будут встречаться в последовательности А, В, C1 , D1 (этот выбор может не быть определенным только в случае равенства AB = CD, когда прямые АС и BD параллельны). Обозначим через α ту из дуг АВ данной окружности К, на которой лежат точки С1, D1, через β —другую дугу АВ и через γ —ту из дуг C1D1, на которой нет точек А, В. Далее, обозначим через М1 точку пересечения прямых АС1 и BD1. Точка M1 лежит внутри К. Пусть К1—окружность, описанная около /\ АВМ1 (рис. 133). Докажем, что при любом сдвинутом положении хорды CD точка пересечения прямых АС и BD будет находиться на К1
Pис. 133
Пока обе точки С, D лежат на дуге α , точка М будет находиться внутри К, а тогда
/ AMB = 1/2(β + γ). (1)
Если же хотя бы одна из точек С, D попадет на дугу β, то точка М будет лежать вне К и тогда
/ AMB = 1/2(α — γ). (2)
В первом случае М лежит на дуге АМ1В окружности К1, так как согласно (1) / АМВ не зависит от положения CD и, значит, равен / АМ1В. Во втором случае, ввиду того что сумма правых частей (1) и (2) равна
1/2(α + β) = 1/2 • 2π = π,
точка М лежит на внешней относительно К дуге АВ окружности K1.
Очевидно, верно и обратное, т. е. любая точка М окружности K1 может быть получена при надлежащем выборе положения хорды CD.
________________________________________________
129. Обозначим данную окружность через О и данную прямую через L (рис. 134).
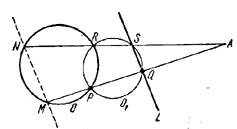
Pис. 134
Пусть М—вторая точка пересечения прямой PQ с O. Возьмем какую-нибудь проходящую через точки Р и Q окружность О1, которая пересекает второй раз окружность О в точке R и прямую L в точке S. Пусть N—вторая точка пересечения прямой RS с окружностью О.
Докажем, что MN | | L. Для этого воспользуемся следующей известной теоремой планиметрии: если даны окружность и точка А, то для любой прямой, проходящей через А и пересекающей эту окружность в точках А1 и А2, произведение отрезков АА1•АА2 есть величина постоянная, не зависящая от выбора прямой.
Обозначим через А точку пересечения прямых PQ и RS. Сначала применим упомянутую теорему к окружности О, точке А и прямым АР и AR. Так как АР пересекает второй раз О в точке М, a AR в точке N, то
AM•AP = AN•AR. (1)
Теперь применим ту же теорему к окружности О1, точке А и тем же прямым. Так как АР пересекает второй раз O1 в точке Q, a AR в точке S, то
AQ•AP = AS•AR. (2)
Из (1) и (2) следует равенство
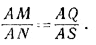 (3) (3)
Из равенства (3) в силу теоремы, обратной теореме о пропорциональности отрезков, отсекаемых на сторонах угла параллельными прямыми, следует, что MN | | QS, что и требовалось доказать.
Таким образом, для любой окружности типа О1 точка N может быть определена как вторая точка пересечения прямой, проходящей через М и параллельной L, с окружностью О. Это построение определяет точку N однозначно независимо от выбора окружности О1. Следовательно, всевозможные прямые RS, получаемые для различных окружностей О1, пересекают окружность О в точке N.
Исключительные случаи, когда из (1) и (2) не следует (3), а именно когда совпадают точки R и Р или точки Q и S или когда PQ | | RS, можно рассматривать как предельные для общего случая и пользоваться соображениями непрерывности.
________________________________________________
|