ГЛАВА  7

СТЕРЕОМЕТРИЯ

ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО

Ответы и решения

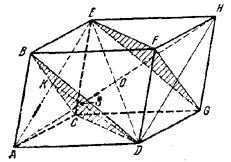
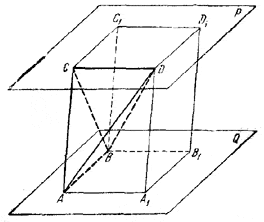
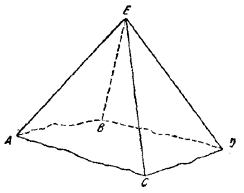
222. Пусть число боковых граней пирамиды равно п. Соединим произвольную точку О, взятую в плоскости ее основания, со всеми вершинами и рассмотрим п треугольных пирамид с общей вершиной в точке О. Очевидно, что объем V данной пирамиды равен сумме объемов  получившихся  треугольных  пирамид.   Имеем:

V = ¹/₃S ( r₁ + r₂ + ...+ r_n ).

где  r₁ , r₂ , ..., r_n — расстояния от  точки О до боковых граней, а S — площадь боковой грани.

Следовательно,  r₁ + r₂ + ...+ r_n = ^3V/_S есть величина постоянная, не зависящая от положения точки О в плоскости основания, что и требовалось доказать.

______________________________________________

223. Рассмотрим   две   плоскости, заштрихованные   на рис. 226, и   треугольник   ADE  в   плоскости   Р,   проходящей через вершины A,  D, Н, Е данного параллелепипеда.

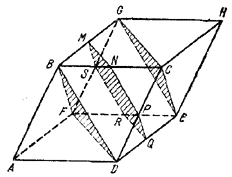
рис. 226

Плоскость Р пересекает плоскость /\ BCD по прямой KD, которая проходит через точку К пересечения диагоналей параллелограмма АВЕС, и следовательно, отрезок KD есть медиана /\ AED. Очевидно, что АР есть также медиана  /\  AED. Поэтому интересующая нас точка S есть точка пересечения   медиан   /\  AED  и, значит,

AS = ²/₃AО = ¹/₃AH,

что и требуется.

______________________________________________

224. Проведем  указанную   в   задаче   плоскость   через вершины B,   D, F (рис. 227)   и   параллельную  ей   плоскость  через  вершины C,  Е, G.

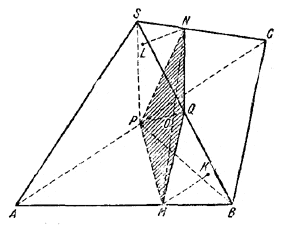
рис. 227

Обе плоскости образуют в пересечении   с   параллелепипедом   равносторонние   и   равные   треугольники.   Длину  стороны   каждого из этих треугольников обозначим через а. Если теперь, через середину одного из шести ребер, соединяющих вершины двух указанных треугольников, например через середину N ребра ВС, — провести плоскость, параллельную двум указанным плоскостям, то она даст в сечении с параллелепипедом шестиугольник MNPQRS, все стороны которого, очевидно, окажутся равными  ^a/₂ . Заметим еще, что MN || DF и NP || BD. Поэтому /  MNP дополняет /   BDF до 180° и, следовательно, /   MNP = 120°. Аналогично устанавливаем, что и остальные углы шестиугольника равны 120°.

______________________________________________

225. Пусть SABC — данный тетраэдр, Р и Q — середины   противоположных ребер АС и SB, MPNQ — некоторое сечение тетраэдра, содержащее отрезок PQ  (рис. 228).   

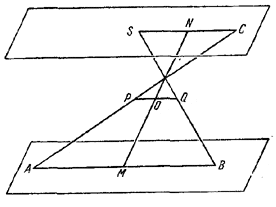
рис. 228

Рассмотрим   плоское   сечение SPB,   которое,   очевидно, разбивает тетраэдр  на   две   равновеликие части. Задача будет решена, если мы докажем, что пирамиды SPQN и MPQB равновелики.

Опустим на плоскость SPB перпендикуляры из точек М и N и их основания обозначим соответственно через К и L. Так как треугольники   PQB  и   SPQ   равновелики, то   для   решения  задачи достаточно показать, что LN = MK.   Мы  установим  это   равенство, доказав, что

MO = NO.                                            (1)

Рассмотрим с этой целью пару  параллельных   плоскостей,   в   которых лежат скрещивающиеся  прямые  SC и АВ (рис. 229).

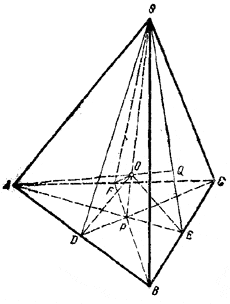
рис. 229

Так как отрезок   PQ   соединяет   середины  отрезков АС   и   SB, то  он, очевидно,  лежит в плоскости, параллельной данным плоскостям и отстоящей от них на равном расстоянии. В силу этого отрезок MN, пересекаясь с отрезком PQ, разделится точкой пересечения пополам.

______________________________________________

226. Пусть SABC—данная пирамида (рис.230).

рис.230

Опустим из вершины S на грань ABC высоту SP и проведем, кроме того, из той же вершины высоты SO, SE и SF остальных трех граней. Легко видеть, что треугольники SPD, SPE и SPF в силу равенства углов SDP, SEP и SFP равны между собой (ср. с задачей 167).

Проведем далее через ребра АВ, ВС и АС плоскости, делящие соответствующие двугранные углы пополам. Эти плоскости пересекаются в точке О, равноудаленной от всех четырех граней пирамиды и, следовательно, являющейся центром вписанного в пирамиду шара. Легко видеть, что в рассматриваемом случае в силу отмеченного равенства треугольников точка O окажется на высоте пирамиды SP. Повторяя рассуждения, мы установим, что все высоты пирамиды пересекаются в   точке О. Используя этот факт, мы  можем утверждать, что, например,   треугольники APS и SPE лежат в одной плоскости и, следовательно, отрезки АР и РЕ расположены на одной прямой. Поэтому АЕ есть одновременно биссектриса и высота /\  ABC. По аналогичной причине и остальные биссектрисы /\  ABC являются его высотами. Следовательно, /\  ABC равносторонний. Повторяя рассуждение, мы  установим, что все грани пирамиды представляют   собой  равносторонние   треугольники, что и завершает доказательство.

______________________________________________

227. Пусть отрезок АВ лежит в плоскости Q, а   отрезок CD — в плоскости   Р   и   пусть Р || Q (рис. 231).

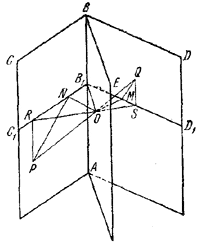
рис. 231

Проведем через точку А прямую,   параллельную  CD,  и отложим отрезок AA₁ = CD. На сторонах АВ и АА₁ построим параллелограмм АВВ₁А₁. Аналогичное построение сделаем в плоскости Р. Соединив А с С, В с C₁ , А₁ с D и B₁ с D₁ , получим параллелепипед ABB₁A₁DCC₁D₁. Рассматривая грань АСВ в качестве основания пирамиды DACB, мы видим, что объем пирамиды равен ¹/₆ объема параллелепипеда. Так как, однако, объем параллелепипеда сохраняется при перемещении отрезков (не изменяются площадь основания АВВ₁А₁ и высота — расстояние между плоскостями Р и Q), то сохраняется и объем   пирамиды.

______________________________________________

228. Пусть Р и Q — точки   пересечения   данной   прямой    с   гранями  СВА   и   DBA  двугранного  угла   (рис. 232).

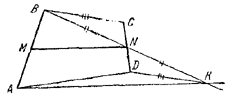
рис. 232

Проведем   через ребро АВ биссекторную плоскость ABE, а затем через точку О  ее пересечения  с   прямой PQ   проведем   плоскость C₁B₁D₁, перпендикулярную к ребру АВ. Пусть, далее, OM_|_B₁D₁, ON _|_B₁C₁ и пусть SR— проекция PQ на плоскость D₁B₁C₁, так что при этом QS _|_ B₁D₁, a PR _|_ B₁C₁. Если точки P и Q одинаково удалены  от   ребра, т. е.

B₁R = B₁S,                     (1)

то треугольник B₁RS— равнобедренный, SO = RO и, следовательно, QO = PO как наклонные, имеющие равные проекции. Учитывая еще, что по построению

МО = NO,                     (2)

мы сможем заключить, что треугольники OMQ и ONP прямоугольные и равные. Отсюда следует равенство углов:

/  MQO = /  NPO                (3)

Итак, в одну сторону утверждение доказано.

Если,    наоборот,   выполнено   равенство  углов    (3),   то   в   силу   (2)   имеет место   равенство   треугольников   QMO   и   PNO.   Вследствие   этого QO = PO   и,   значит,   SO = OR.   Отсюда   уже следует равенство (1).

______________________________________________

229. Соединим точки В и С, А и D отрезками прямых (рис. 233).

рис. 233

Через   точку   А   проведем   прямую   параллельно   MN   до встречи в точке К с прямой, проходящей через В и N. Заметим, что AK = 2MN, так как MN — средняя линия в треугольнике АВК.  Далее, /\BNC  = /\KND, ибо BN = NK, CN=ND a /  BNC = /  KND. Поэтому DK =  ВС. Из треугольника ADK следует:

DK + AD > AK=2MN

(здесь   существенно, что  точка   D  не  лежит на прямой АК, иначе пришлось бы поставить знак >). Итак,

BC+AD > 2MN,

что и требовалось доказать.

______________________________________________

230. Пусть   А, В,   С   и   D — произвольные  точки,   лежащие  на ребрах  четырехгранного  угла   с   вершиной  E (рис. 234).

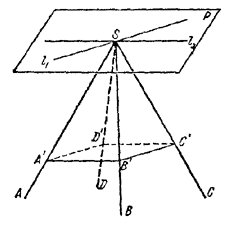
рис. 234

Докажем, например, что

/  CED < /  СЕА+/  АЕВ+ /  BED.                   (1)

Проведем плоскость СЕВ. По свойству плоских углов трехгранного угла

/  CED < /  CEB + /  BED                           (2)

и по той же причине

/  СЕВ < /  СЕА +  /  АЕВ.                           (3)

Из неравенств  (2)  и  (3)   следует (1). Неравенство (1), таким образом, доказано.

Легко понять, что наше рассуждение сохраняет силу и в том случае, когда четырехгранный угол не является выпуклым, т. е. когда  ребро  ED  оказывается   по  другую сторону плоскости СЕВ.

______________________________________________

231. Пусть дан выпуклый четырехгранный угол с вершиной S (рис. 235).

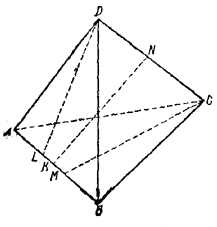
рис. 235

Продолжим плоскости BSC и ASD до их пересечения по прямой l₁. Плоскости ASB и DSC продолжим до пересечения по прямой l₂. Прямые l₁ и l₂, очевидно, не совпадают (в противном случае все грани при продолжении проходили бы через одну прямую).

Обозначим через Р плоскость, содержащую прямые l₁ и l₂. Легко показать, используя выпуклость четырехгранного угла, что плоскость Р имеет с данным углом лишь одну общую точку пересечения S, так что весь угол располагается по одну сторону от плоскости Р (впрочем, этот факт почти очевиден).

Покажем теперь, что всякая пересекающая угол плоскость, параллельная плоскости Р, образует с ним в сечении параллелограмм. В самом деле, такая плоскость пересечет, в силу сказанного, все четыре ребра четырехгранного угла. Обозначив соответствующие точки пересечения через А', В', С', В', заметим, что A'D' || В'С', так как оба эти отрезка порознь параллельны l₁, по аналогичной причине А'В' || D'C'.

Следовательно, четырехугольник A'B'C'D' — параллелограмм, что и требовалось доказать.

______________________________________________

232.  Пусть  DL  и   СМ — высоты треугольников ADB и АСВ, опущенные на общее основание АВ (рис. 236).

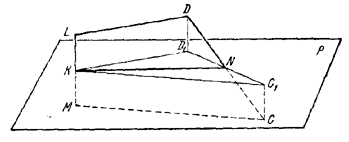
рис. 236

Так  как  эти  треугольники  равновелики, то  DL= CM. Пусть еще KN—общий перпендикуляр к скрещивающимся   ребрам   АВ и DC. Проведем   через  отрезок   КN  плоскость  Р, перпендикулярную ребру   АВ. Четырехугольник  LMCD спроектируем на плоскость Р (рис. 237).

рис. 237

Так как отрезки DL и СМ проектируются без изменения длин (они параллельны плоскости Р), а отрезок LM— в точку, то в проекции получается равнобедренный треугольник KD₁C₁. По построению KN _|_ DC, следовательно, KN _|_ D₁C₁ и значит, KN — высота /\KD₁C₁. Поэтому N — середина отрезка D₁C₁, а значит, и отрезка DC.

Таким образом, в условиях задачи основание общего перпендикуляра к двум скрещивающимся ребрам пирамиды делит эти ребра пополам.

Из рис. 237 легко заметить, что LK = KM,  ибо DD₁ = CC₁.
Поэтому  (см. рис. 236) AL = BM и из равенства прямоугольных треугольников ALD  и  ВМС следует, что

AD = BC.

Аналогично доказывается, что AC = BD и АВ = DC. Следовательно, все грани равны между собой, как треугольники, имеющие по три равные стороны.

______________________________________________