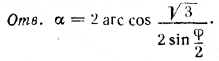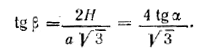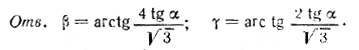|
|
|
|
|
ГЛАВА 2 МНОГОГРАННИКИ Ответы и решения |
|
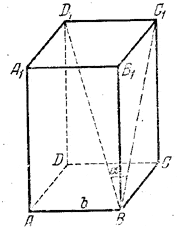
130. Проекция диагонали BD1(рис. 117) на боковую грань ВСС1В1 есть ВС1.
рис. 117 Поэтому / C1BD1 = α. Из треугольника BC1D1, где D1С1= b, находим BC1= b ctg α. Из треугольника В1С1В имеем
3амечание. Подкоренное выражение cos 2α здесь (ср. замечание 2 к задаче 129) всегда положительно, ибо α < 45°. Действительно,
По В1С1 есть катет, а ВС1—гипотенуза треугольника ВВ1С1. Поэтому tg α < 1, т. е. α <45°.
______________________________________________ 131. Если СВ (рис. 118) есть высота треугольника ABC, опущенная на гипотенузу АВ = с ( на изображении можно провести CD произвольно внутри угла АСВ ), то / CDC1 = β (доказать!).
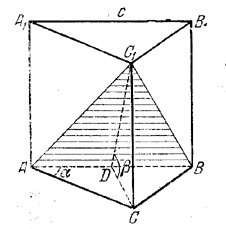
рис. 118 Имеем CD = АВ • sin α cos α =1/2 с sin 2α и H = CC1 = CD • tg β Эти выражения подставляем в формулу V = 1/3SH =1/3 • 1/2 с • CD • H Отв. V = 1/24 с3 sin2 2α tg β. ______________________________________________ 132. Одна из частей призмы есть треугольная пирамида В1АВС (рис. 119).
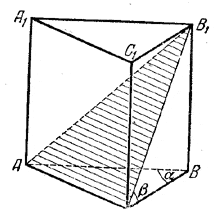
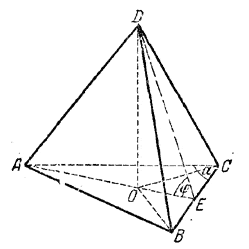
рис. 119 Ее объем V1 = 1/3V, где V — объем призмы. Значит, объем V2 другой части (четырехугольной пирамиды B1A1C1CA ) равен 2/3V Найдем V. По условию ВС + АВ = т, а из треугольника ABC находим BC=AB•cos α. Следовательно,
Площадь основания призмы S равна S = 1/2 • АС • ВС = 1/2 • ВС2 • tg α. Высоту Н = ВВ1 определяем из треугольника ВСВ1, где / ВСВ1 = β (доказать!). Получаем H = BC•tg β.
______________________________________________ 133. Согласно предварительному замечанию к задаче 108, Socн.
= S cos φ = S sin α. С другой стороны, Приравнивая эти два выражения, получим a = 2√S cos α.
рис. 120 Точка О (центр окружности, вписанной в треугольник ABC; рис. 120) лежит на пересечении биссектрис углов треугольника, следовательно, / OCE = α/2 и OE = EC • tg α/2 = a/2 tg α/2 из /\ DOE находим H = OE• tg φ
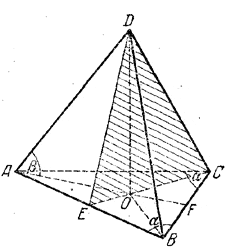
______________________________________________ 134. На рис. 121 OA= OC = R— радиусы окружности, описанной «коло равнобедренного треугольника ABC (АВ = АС = а).
рис. 121 В силу условия α > 45° центр О лежит внутри треугольника AВС (при α < 45° угол ,4 = 180° — 2α был бы тупым, центр описанной окружности лежал бы вне треугольника ABC, и тогда плоскость, проведенная через высоту пирамиды и вершину С, не дала бы никакого сечения пирамиды). Высота пирамиды проходит через центр О см. предварительное замечание ). Из треугольника AOD имеем H = R tg β. Так как по теореме синусов AC = a = 2R sin α, то Найдем теперь основание СЕ сечения из треугольника АСЕ. В нем / CAE = 180° — 2α, a / ACE, лежащий в основании равнобедренного треугольника АОС (АО = ОС = R), равен / CAO = 1/2 / CAE = 90° — α. Значит, / AEC = 3a — 90°. По теореме синусов
Замечание. В знаменателе можно написать (—cos 3α); но угол 3α заключен между 135° и 270°, так как 45° < α < 90°; таким образом, (—cos 3α) есть положительное число. Поэтому при вычислениях с таблицами удобнее иметь дело с углом 3α—90°, заключенным между 45° и 180°.
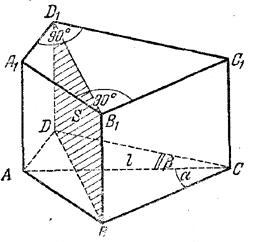
______________________________________________ 135. 1) Найдем площадь Q основания призмы (рис. 122).
рис. 122 Имеем: Q = S1 + S2, где S1 — площадь прямоугольного треугольника ABC, a S2 — площадь прямоугольного треугольника ADC,
2) Найдем высоту Н призмы из условия S = BD • H. Так как в четырехугольнике ABCD сумма углов при вершинах В и D равна 180°, то около него можно описать окружность, диаметром которой будет диагональ АС, потому что на нее опираются прямые вписанные углы. Из треугольника BCD, вписанного в эту окружность, находим (по теореме синусов) BD = AC • sin / DCB = l sin (α + β), Следовательно,
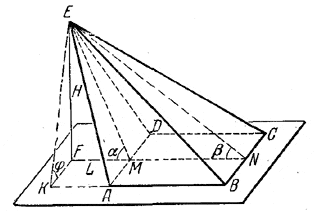
Отв. V = 1/2 S • l cos (α — β). ______________________________________________ 136. Грани ADE и ВСЕ (рис. 123) — равнобедренные треугольники.
рис. 123 Плоскость EMN (М и N— середины ребер AD и ВС) перпендикулярна к ВС и AD и проходит через высоту EF пирамиды (доказать!). По условию внешний угол α = / EML треугольника EMN — острый. Поэтому высота EF пересекает продолжение MN. Чтобы определить V, найдем сторону АВ квадрата ABCD. Имеем AB = MN =NF — MF = H (ctg β — ctg α). Следовательно, V = 1/3 АВ2 • Н = 1/3 Н3(ctg β — ctg α)2 Построим линейный угол φ двугранного угла, под которым грань ABE наклонена к основанию. Для этого пересечем двугранный угол плоскостью EFK, перпендикулярной к ребру АВ. Чтобы изобразить ее, надо провести FK || AD до пересечения с продолжением ребра АВ (доказать!). Из треугольника EFK находим
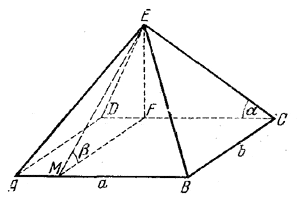
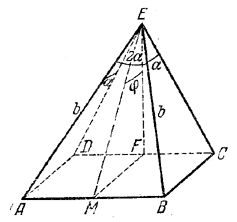
______________________________________________ 137. Высота EF пирамиды (рис. 124) лежит в грани CED, перпендикулярной к плоскости основания.
рис. 124 Плоскость, проведенная через EF перпендикулярно к ребру АВ, пересекает основание пирамиды по прямой MF || ВС, а боковую грань АЕВ — по прямой ME, перпендикулярной к АВ ( / EMF = β ). Прямые AD и ВС перпендикулярны к плоскости DEC, так что / BCE = 90° и / ADE=90° (все это надо доказать). Найдем высоту H = EF. По условию EF+EM = m; кроме того,
Далее из прямоугольного треугольника DEC находим
Наконец, находим b = BC = MF = H ctg β = H tg α. Следовательно,
Сумма S1+S2 площадей боковых граней ВЕС и AED равна
______________________________________________ 138. а) Способ изображения. Высоту EF (рис. 125) проводим в середину F стороны DC. Соединяем вершину Е с серединой М стороны АВ. Тогда φ = / FEM есть изображение угла между гранями ABE и DCE (доказать!).
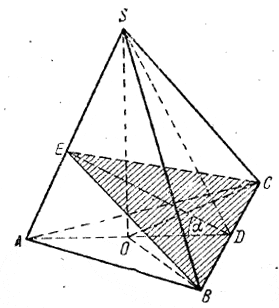
рис. 125 б) Решение. Треугольник ВСЕ — прямоугольный, и в нем / BEC = α (доказать!). Значит ВС = b sin α. Из треугольника ABE имеем AB = 2b sin α и ME = b cos α. Из треугольника MFE, где MF = BC= b sin α, находим FE = √ME2—MF2 = b √cos2α — sin2α = b √cos2α . Замечание. Подкоренное выражение cos 2α здесь всегда положительно, так как 2α<90°. Действительно, сумма двух плоских углов трехгранного угла при вершине В Угол φ лучше всего найти по его синусу. Отв. V = b3 sin2α √cos2α ; φ = arc sin (tg α). ______________________________________________ 139. Плоскость ВСE (рис. 126) проведена через сторону ВС перпендикулярно к ребру AS. Двугранные углы между боковыми гранями (все они равны) измеряются углом ВEС = φ. Треугольник ВЕС — равнобедренный.
рис. 126 Чтобы определить площадь S сечения и угол φ, достаточно найти DE (D — середина ВС). Для этого последовательно находим BS (из треугольника BSD, где BD = a/2 и / BSD = α/2 ). Затем BE (из треугольника BSE, где / BSE = α) и, наконец, DE=√BE2—BD2 . Получаем
Замечание 1. Сумма плоских углов при вершине S всегда меньше 360°. Поэтому 0<α<120°. При этом условии 2cosα/2> 1, т. е. Замечание 2. Если α>90°, т. е. угол ASB при вершине боковой грани тупой, то высота BE треугольника ASB пересечет продолжение основания, и плоскость ВЕС не даст никакого сечения пирамиды. Между тем формула
и при тупом угле α (меньшем 120°, см. замечание 1) даст определенное значение S. Отв. φ = 2 arc sin ( 1/2 sec α/2);
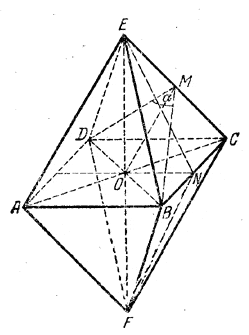
______________________________________________ 140. Все восемь граней октаэдра — равносторонние треугольники, так что
рис. 127 Четырехугольник ABCD — квадрат.
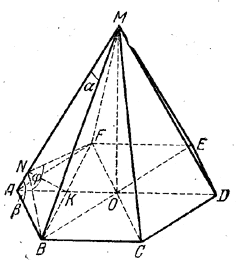
______________________________________________ 141. Об изображении правильного шестиугольника см. замечание к задаче 89. Равнобедренные треугольники ВМА и FMA (рис. 128) равны.
рис. 128 Поэтому их высоты, опущенные из вершин В и F, пройдут через одну и ту же точку N их общей стороны и будут равны: BN=FN. Угол BNF равен φ (доказать!). Угол β = / BAM выражается через искомый угол α = / ВМА формулой β = 90° — α/2. Найдем сначала тригонометрическую функцию угла β. Из прямоугольного треугольника ABN имеем sin β = BN/a (а — сторона основания). Из равнобедренного треугольника BNF находим Но ВК = a√3/2 (как высота равностороннего треугольника АВО). Следовательно,
Замечание. Двугранный угол при ребре правильной шестиугольной пирамиды всегда больше, чем /
FAB (сравнить треугольники BNF и BAF), т. е. больше 120°. Поэтому величина
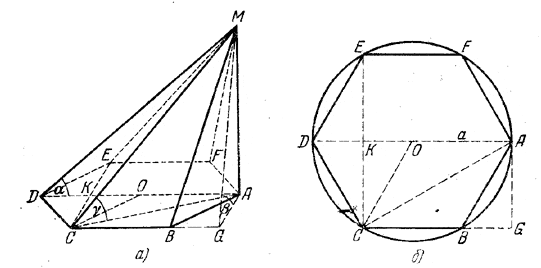
______________________________________________ 142. Грани AMF и АМВ (рис. 129, а), проходящие через ребро AM (перпендикулярное к плоскости ABCDEF), образуют с плоскостью основания прямые углы.
рис. 129 Найдем общую величину β углов, образуемых гранями EMF и СМВ с плоскостью основания. Опустим из А перпендикуляр AG на прямую СВ (изображение этой прямой должно быть параллельно СЕ, рис. 129, б). Тогда β = / AGM (доказать!). Имеем tg β = H/AG , где AG = СК = a√3/2. (рис. 129, б). Но из треугольника AMD имеем tg β = H/2a ; следовательно,
Так как AC_|_DC (доказать!), то γ = / ACM есть линейный угол для двугранного угла, под которым грань DCM (и DEM) наклонена к плоскости основания. Из треугольника АСМ имеем tg γ = H/AC, где AС = а√3 (рис. 129, б).
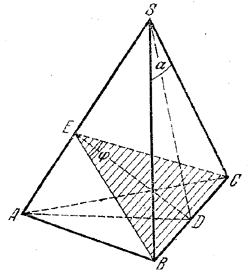
______________________________________________ 143. Через прямую линию можно продести плоскость, перпeндикулярную к другой прямой, только в том случае, если эти прямые перпендикулярны.
рис. 130 Докажем, что BC_|_AS (рис. 130). Проведем плоскость ASO через ребро AS и высоту SO. Так как А и О принадлежат плоскости ASO и одновременно плоскости основания ABC, то эти плоскости пересекутся по прямой АО, т. е. по высоте AD равнобедренного треугольника ABC. Треугольники OCD и OBD равны (доказать!), поэтому ОВ = ОС; следовательно, наклонные SC и SB тоже равны, а значит, прямая SD, являющаяся медианой равнобедренного треугольника BSC, служит и его высотой. Так как прямые AD и SD, по доказанному, перпендикулярны к ребру ВС, то ребро ВС перпендикулярно к плоскости ADS, a значит, и к прямой AS, лежащей в этой плоскости, что и требовалось доказать. Чтобы провести через ВС плоскость, перпендикулярную к AS, достаточно опустить перпендикуляр DE на прямую AS. Плоскость ВЕС перпендикулярна к ребру AS, так как две прямые, лежащие на ней (DE и ВС), перпендикулярны к AS. Плоскость ADS, перпендикулярная к ребру ВС, в пересечении с двугранным углом α дает угол ADE (линейный угол этого двугранного угла). Треугольник ASD — равнобедренный (так как высота SO проходит через середину основания AD). Следовательно, / ASD = 2 / ASO = 2α (/ ASO = / ADE = α как углы с перпендикулярными сторонами). Отношение объема V; пирамиды SBCE к объему V пирамиды АВСЕ (эти пирамиды имеют общее основание ВСЕ) равно отношению высот, т. е. V1 : V= SE : AE. Из треугольника DSE имеем SE = DE • ctg / ESD = DE • ctg 2α; из треугольника AED находим AE = DE • tg α;. Следовательно, V1 : V= ctg2α : tg α. Oтв. V1 = V ctg α ctg 2α. ______________________________________________ |
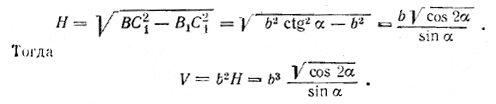
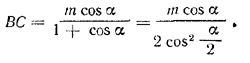
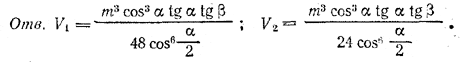
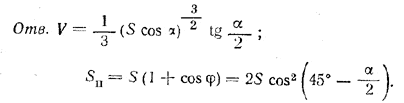
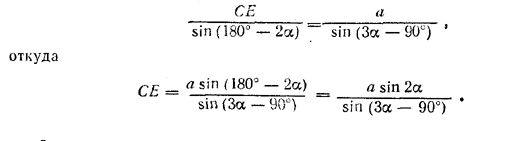
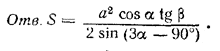
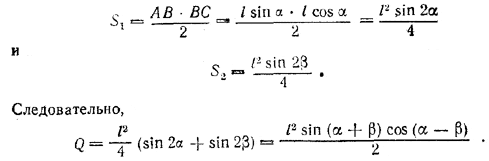
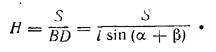
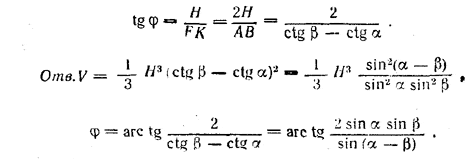
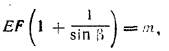 откуда
откуда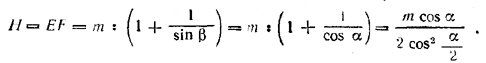
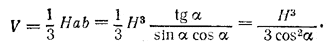
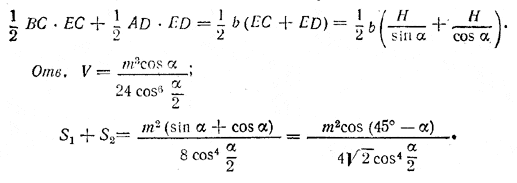
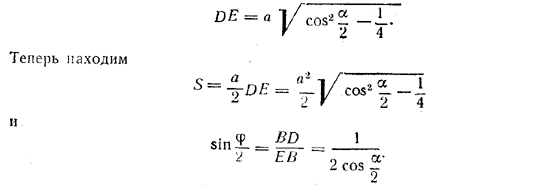
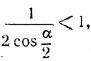 так что уравнение
так что уравнение 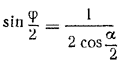 всегда имеет решение.
всегда имеет решение.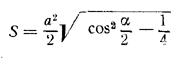
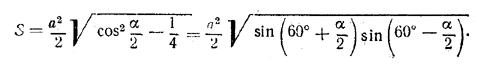
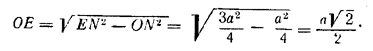
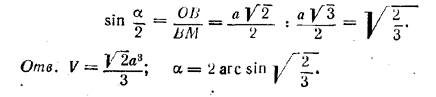
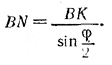 .
.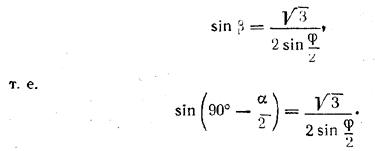
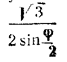 всегда меньше единицы.
всегда меньше единицы.