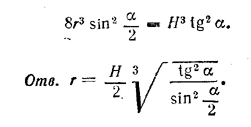|
|
|
|
|
ГЛАВА 3 КРУГЛЫЕ ТЕЛА Ответы и решения |
|
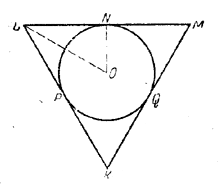
250. Высота призмы равна диаметру 2R вписанного шара. Если через центр О шара провести плоскость, параллельную основаниям призмы, то в сечении призмы получим равносторонний треугольник КLМ (рис. 224), равный основанию призмы, а в сечении шара — большой круг PNQ, вписанный в треугольник KLM.
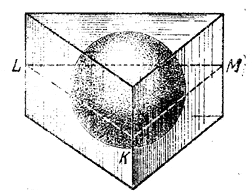
Для наглядности рядом с рис. 224 помещаем рисунок 224а — наглядное изображение рассматриваемого тела. Такие «параллельные» рисунки будут даны и в некоторых следующих задачах. Выполнение их учащимися не обязательно, хотя и очень полезно.
рис. 224 рис. 224 a Из треугольника LON, где ON=R и /
NLO = 30°, найдем LN = R√3 . Следовательно, LM= а =2R√3. Боковая поверхность Sбок. призмы равна Sбок.= 3aH= 12R2√3. Площадь основания Следовательно, Sп. = 12R2√3 + 6R2√3 = 18R2√3 Поверхность же шара равна 4πR2. Oтв. Искомое отношение равно ______________________________________________ 251. а) Способ изображения. Центр О1 шара, вписанного в пирамиду (если в эту пирамиду можно вписать шар), должен отстоять на равных расстояниях от боковой грани ВЕС и от основания ABCD (рис. 225).
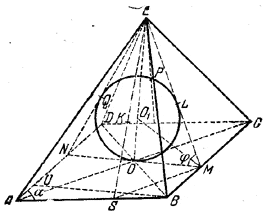
рис. 225 Поэтому он должен лежать на биссекторной плоскости двугранного угла φ при ребре ВС. Точно так же О1 лежит на биссекторных плоскостях двугранных углов φ при ребрах АВ, AD, DC. Значит, все боковые грани пирамиды O1ABCD (не изображенной на чертеже) наклонены к плоскости основания под одним и тем же углом φ/2 Следовательно, высота О1О пирамиды O1ABCD проходит через центр О окружности, вписанной в ромб ABCD (см. замечание к задаче 108). Через тот же центр проходит высота ЕО данной пирамиды. Значит, центр O1 шара лежит на высоте EO. Точка касания шара с плоскостью грани, ВЕС есть основание L перпендикуляра, опущенного из центра О1 шара на плоскость ВЕС. Отсюда следует, что плоскость O1EL перпендикулярна к грани ВЕС (доказать!). Вместе с тем плоскость O1EL перпендикулярна к плоскости основания ABCD (так как проходит через высоту EO). Следовательно, плоскость O1EL перпендикулярна к ребру ВС. Значит, прямая MN, по которой пересекаются плоскости O1EL и ABCD, есть высота ромба (проведенная через его центр О). То же имеет место для остальных трех точек касания с боковыми гранями (K, Q и Р). Отсюда вытекает следующее построение. Изображаем высоту NOM ромба ABCD (желательно, чтобы она была горизонтальной), строим сечение NEM (равнобедренный треугольник) и изображаем окружность, вписанную в треугольник NEM. Точки L и Q, в которых эта окружность коснется сторон ME н NE, будут точками касания шара с гранями ВЕС и AED. Чтобы изобразить точку К, проведем MS || АС. Тогда прямая OS (не показанная на чертеже) изображает другую высоту ромба (доказать!). Проводим прямую ES и через точку L проводим (не изображенную) прямую LK || MS. Четвертая точка Р строится аналогично. Из этого построения следует, что шар с центром О1 и радиусом R = O1L действительно вписан в пирамиду. б) Решение. Из треугольника МОО1 находим ОМ = OO1 ctg φ/2 = R ctg φ/2, так что Н = ОЕ = ОМ • tg φ = R ctg φ/2 tg φ. Далее из треугольника BUA (где BU || МN) находим
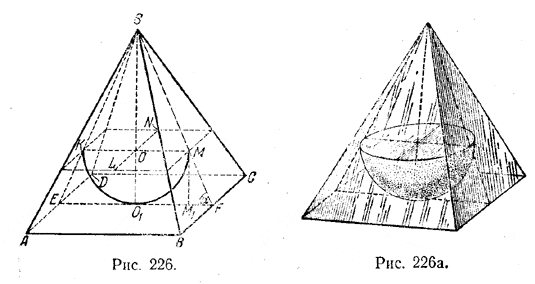
______________________________________________ 252. а) Способ изображения. Центр О экватора полушара (т. е. круга, ограничивающего полушар; рис. 226) лежит па высоте SO1 пирамиды.
Так как OM = OO1 = r , то точка М лежит на биссектрисе О1М угла ОО1М1. Отметив точку М как пересечение O1М с SF, изображаем сечение KLMN, параллельное основанию. Середины К, L, М, N сторон сечения являются точками касания экватора с боковыми гранями. Полукруг КО1М есть сечение полушара плоскостью ESF. б) Решение. Сторона основания а равна a = EF = 2 • O1F = 2 (O1M1+M1F). Но O1M1 = OM = r, a M1F = MM1 • ctg α = r ctg α. Значит, a = 2r (1+ctg α). Имеем
Здесь Socн. = а2 = 4r2 (1+ctg α)2 .
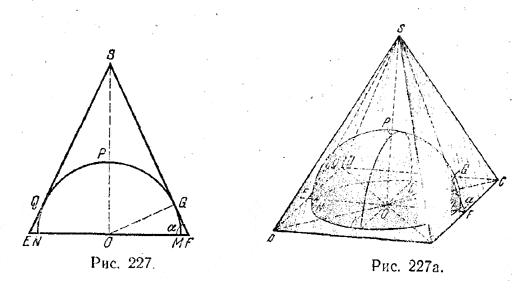
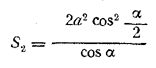
______________________________________________ 253. Плоскость ESF (рис. 227) даст в пересечении с полушаром полукруг NPM, касающийся апофем пирамиды (в точках Q и G).
Если обозначим сторону основания пирамиды через а, а радиус полушара — через r, то полная поверхность полушара S1 будет S1 = 2πr2 + πr2 = 3πr2 и полная поверхность пирамиды
их отношение
Из /\ OGF имеем OG = OF• sin α, т. е. r = a/2 sin α. Это выражение подставим в предыдущее равенство. Для вычисления объема полушара V найдем r из условия а — 2r = т и ранее найденного равенства r = a/2 sin α. Получим
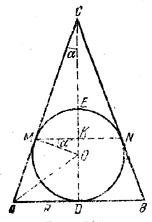
______________________________________________ 254. На рис. 228 изображено осевое сечение конуса и вписанного в него шара. Искомый объем V получается вычитанием объема шарового сегмента MEN из объема конуса MCN.
рис. 228 Следовательно, V = π/3 • МК2 • КС — π • КЕ2 ( r —1/3 КE), где r есть радиус шара. Из треугольника AOD находим r = OD = AD • tg / DAC/2 = R tg (45° — α/2). Теперь из треугольника ОМК, где / ОМК = α (стороны углов ОМК и МСК взаимно перпендикулярны), имеем MK = OM • cos α = r cos α и OK = r sin α. Значит, КЕ = ОЕ— OK = r (1 — sin α). Наконец, КС = МК. • ctg α = r cos α ctg α. Следовательно,
Это выражение можно упростить. Вынесем за скобки (1 — sin α )2, предварительно преобразовав cos4 α; именно, cos4 α =( l — sin2 α )2=( l — sin α )2 (1+ sin α )2. Теперь имеем
Вырал<ение в квадратных скобках равно единице. Получаем
Сюда подставляем найденное выражение r = R tg (45° — α/2). Кроме того, можно использовать формулу 1 — sin α = 2 sin2 (45° — α/2).
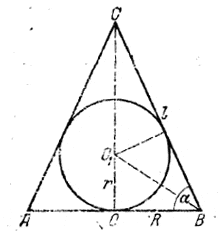
______________________________________________ 255. При обозначениях рис. 229 условие задачи выражается равенством πR ( l + R ) = n • 4πr2.
рис. 229 Из треугольника OBO1 находим r = R tg α/2 , а из треугольника ВОС имеем ВС = l = R/cos α Предыдущее равенство по сокращении на πR2 примет вид 1 + 1/cos α = 4n tg2 α/2 Применим формулу
Будем иметь уравнение
Положив tg α/2 = z, получим
(Освобождаясь от знаменателя, мы могли бы внести лишнее решение ( tg2 α/2 = 1 ) , но такого решения мы не получаеи: оно не удовлетворяет исходному уравнению.) Отсюда видно, что при n < 2 задача не имеет решения (под корнем отрицательное число). При n > 2 оба значения величины z 2 положительны Так как величина tg α/2 должна быть положительной, то можем иметь только два решения:
Так как угол α/2 меньше 45°, то tg α/2 должен быть меньше единицы; знaчит, должно быть z 2 < 1. Но это неравенство всегда соблюдено, ибо
Отв. Задача имеет решение только при n > 2. При п >2 имеем два решения:
при п =2 оба решения совпадают ______________________________________________ 256. При обозначениях рис. 229 имеем 1/3 πR2H = n • 4/3 πr Подставляя сюда r = R tg α/2 и H = R tg α, получим уравнение tg α = 4n tg3 α/2. Применив формулу
и обозначив tg α/2 через z, получим уравнение
Оно распадается на два, но одно из них (z = 0) не согласуется с условием (угол α не может равняться нулю). Другое уравнение приводится к виду z4— z2 + 1/2n = 0, т. е. совпадает с уравнением предыдущей задачи. Получаем два решения:
другое дает tg α/2 = sin 22°30' ≈ 0,3827 (отсюда α1 ≈ 85°28' и α2 ≈ 41°53'). Отв. Тот же, что в предыдущей задаче. При п = 4 имеем α1 =2 arc tg (cos 22° 30') (≈85° 28'); α2 = 2arctg (sin 22°30') (≈41° 53'). ______________________________________________ 257. Площадь осевого сечения есть RH. Полная поверхность πRl + πR2. По условию Если β — угол между осью и образующей, то R = l sin β и H = l cos β. Подставляя эти выражения, получим
Это уравнение можно решить различными способами; короче всего применить формулу
Отсюда можно определить угол 45° — β/2 а затем и угол β. Однако не при всяком п задача имеет решения. Действительно, угол β заключен в границах от 0 до 90°; значит, угол 45° — β/2 заключен между 0 и 45°, т. е. величина n/π = =ctg ( 45° — β/2 ) непременно должна быть больше единицы, т. е. должно быть n > π. При n = 1, 2, 3 задача не имеет решения. Замечание. Уравнение
можно решить еще так. Представим его в виде n/πcos β —1 = sin β, возведем в квадрат обе части равенства и заменим sin2 β через 1— cos2 β. Получим два решения: одно из них, cos β = 0, будет посторонним (оно является решением уравнения n/πcos β —1 = —sin β; другое решение
совпадает с предыдущим. Однако теперь легко прийти к ошибочному выводу, что задача имеет решение также и при п = 1, 2, 3. Ведь при любом положительном значении п величина Ошибка этого рассуждения состоит в следующем. Из соотношения Отсюда видно, что должно быть п > π (в противном случае угол β будет отрицательным, что невозможно). Отв. Если п < π, то задача не имеет решения. Если п > π, то
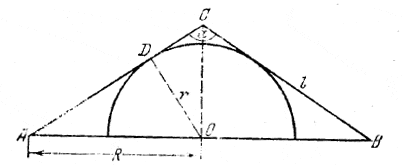
______________________________________________ 258. При обозначениях рис. 230 имеем
рис. 230 Находим (из треугольника AOD) r = R cos / AOD = R cos / ACO = R cos α/2 и (из треугольника АОС)
Сокращаем дробь на 1 + sin α/2 (эта величина не равна нулю). Уравнение приводится к виду sin2 α/2 — sin α/2+ 5/36 = 0 Отв. α1 = 2 arc sin 5/6 (≈112° 53') и α2 = 2 arc sin 1/6 (≈19° 11'), ______________________________________________ 259. При обозначениях предыдущей задачи имеем соотношение π/3R2H = 4/3•2/3 πr3. Обозначим искомый угол через β (на рис. 230 β = α/2). Тогда r = R cos β и H = R ctg β. Из предыдущего соотношения получим 3ctg β — 8 cos3 β = 0. Помножив обе части этого уравнения ни tg β (эта величина по смыслу задачи не может равняться нулю), получим уравнение 3 — 8sin β cos2 β = 0, откуда 8 sin3 β —8 sin β + 3=0. Для решения этого кубического уравнения придется применить какой-либо искусственный прием. Так, левую часть удается разложить на множители: 8 sin3 β —8 sin β + 3 = (8 sin3 β — 1) — (8 sin β — 4) = = [(2sin β)3—1] — 4 (2 sin β — 1) = (2 sin β — 1) [(2 sin β)2+2 sin β + 1— 4]. Следовательно, найденное уравнение распадается на два. Из первого находим sin β = 1/2 , а из второго решение квадратного уравнения не годится.) Проверка показывает, что оба найденных решения годны.
______________________________________________ 260. По условию боковая поверхность конуса MCN (рис. 231) должна составлять половину боковой поверхности конуса АСВ. Но боковые поверхности этих конусов относятся, как квадраты образующих, т. е.
рис. 231 А так как CN = CO, то Отв. α = 45°. ______________________________________________ 261. По условию задачи объем V шарового сектора CMKN (рис. 232) должен составлять половину объема конуса АСВ.
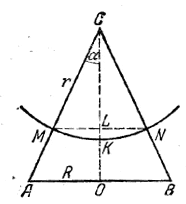
рис. 232 Обозначим отрезок KL через h, а высоту конуса СО через Н. Тогда V = 2/3 πr2h. Получаем равенство 2/3 πr2h = 1/2•1/3 πR2H; т. е. 4r2h = R2H или 4r2h = H3 tg2 α. Величину h выразим через r. Имеем h = LK = СK— CL = r — r cos α = 2r sin2 α/2. Получаем уравнение
______________________________________________ |
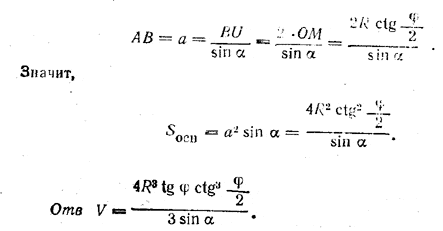

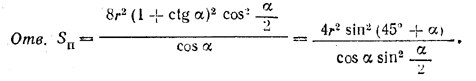
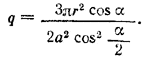
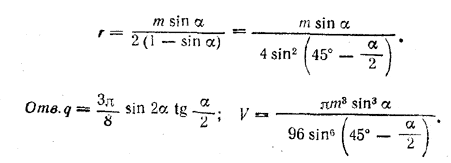
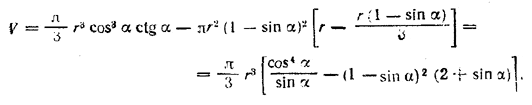
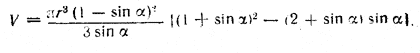
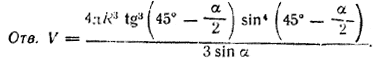
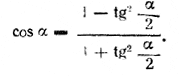
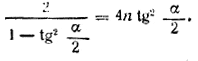
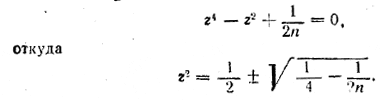
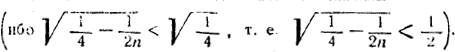
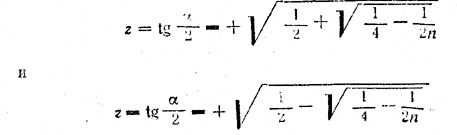
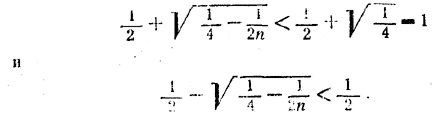
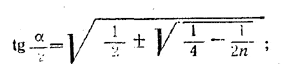
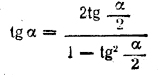
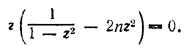
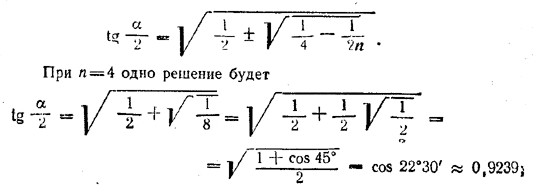
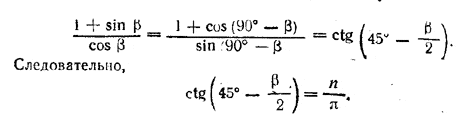
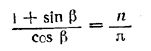

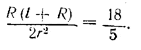
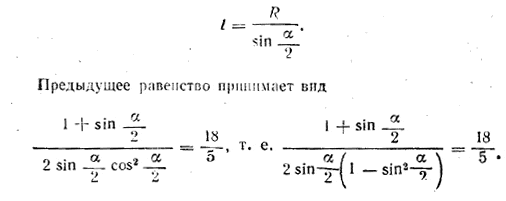
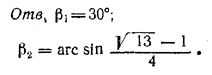
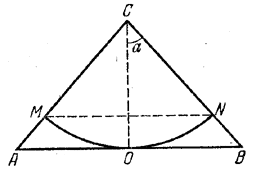
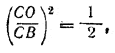 т. е. cos2 α = 1/2
т. е. cos2 α = 1/2