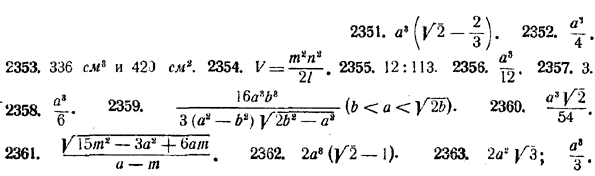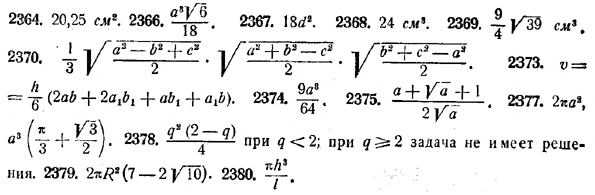ГЛАВА   3

Поверхности и оъемы тел

Группа B

2351.  Два одинаковых куба с ребром, равным а, имеют общий отрезок АВ, соединяющий середины двух противоположных ребер (не  принадлежащих   одной грани), но один куб повернут вокруг этого  отрезка   на   90°  по  отношению  к другому.   Найти  объем общей части этих кубов.

2352.  Даны два  одинаковых   куба с ребром, равным а. Если первый   куб  повернуть   на   90°  вокруг  средней  линии одной из его  граней,   то он совпадет  со   вторым кубом. Найти объем общей части этих кубов.

2353.  В основании прямой призмы лежит треугольник со сторонами  6  см,   8 см  и   10 см .  Некоторое  плоское сечение этой призмы  отсекает от боковых   ребер, проходящих через вершину большего   и   среднего   угла   основания,   отрезки,   равные   12 см  каждый,   а от ребра, проходящего через вершину меньшего угла основания,— отрезок  в   18   см.   Найти объем и площадь полной поверхности  тела,   ограниченного плоскостью основания призмы, плоскостями боковых граней и плоскостью сечения.

2354.  Ребро наклонного параллелепипеда равно l . К нему примыкают две   смежные   грани,   площади   которых   соответственно равны т² и n² и плоскости которых образуют угол в 30°. Вычислить объем параллелепипеда.

2355.   Через   точку,   делящую   ребро правильного тетраэдра в отношении 1:4, проведена плоскость, перпендикулярная к этому ребру.   Найти  отношение объемов полученных частей тетраэдра.

2356.   Боковые  ребра  треугольной   пирамиды имеют одинаковую длину  и  равны  а.  Из  трех  плоских   углов, образованных этими  ребрами  при   вершине  пирамиды,   два   содержат   по  45°, а третий — 60°. Определить объем пирамиды.

2357.   Через  каждое  ребро  правильного  тетраэдра  проведена плоскость,   параллельная   противоположному   ребру. Найти отношение объема полученного параллелепипеда к объему тетраэдра.

2358.   Через  каждые  три   вершины   куба,   расположенные на концах каждой тройки ребер, сходящихся в одной вершине, проведена  плоскость.   Найти объем тела, ограниченного этими плоскостями, если ребро куба равно а.

2359.   Из середины высоты правильной четырехугольной пирамиды  опущен перпендикуляр на боковое ребро, равный а, и перпендикуляр на боковую грань, равный b. Найти объем пирамиды.

2360.  Два   правильных   тетраэдра   соединены  двумя   гранями так,   что  образуют двойную  пирамиду.   Центры  шести   боковых граней этой двойной пирамиды приняты за вершины прямой треугольной   призмы.   Вычислить  объем  этой   призмы,   если   ребро тетраэдра равно а.

2361.  Сторона   основания  правильной  треугольной   пирамиды равна а, площадь ее сечения, имеющего форму квадрата, равна т². Найти отношение боковой поверхности пирамиды к площади основания.

2362.  Два   куба  с  ребром,   равным а, имеют общий отрезок, соединяющий  середины  двух   противоположных граней, но один куб  повернут на 45° по отношению к другому. Найти объем общей части этих кубов.

2363.  Через  концы  трех ребер, выходящих из вершин В, D, A₁ и C₁ куба ABCDA₁B₁C₁D₁ ребро которого равно а, проведены плоскости.  Доказать,   что  полученное тело есть правильный тетраэдр, и вычислить его полную поверхность и объем.

2364.   Через  сторону  основания   правильной четырехугольной пирамиды   проведена  плоскость,   которая  отсекает от противоположной грани треугольник площадью 4 см². Найти боковую поверхность  пирамиды,   которая  отсечена  проведенной плоскостью от данной пирамиды, если   боковая поверхность данной пирамиды равна 25 см².

2365.  Доказать, что объемы двух треугольных пирамид, имеющих по равному трехгранному углу, относятся друг к другу, как произведения длин трех ребер равных трехгранных углов.

2366.  Сторона  основания   правильной  четырехугольной пирамиды равна а, а боковое ребро составляет с высотой угол в 30°. Через  вершину  основания  пирамиды  проведена плоскость, перпендикулярная противолежащему боковому ребру. Эта плоскость разбивает пирамиду на две части. Определить объем части пирамиды, прилегающей к вершине.

2367.   Расстояние между непересекающимися диагоналями двух смежных  боковых граней куба равно d. Определить полную поверхность куба.

2368.   Вычислить объем треугольной пирамиды, у которой два противоположных   ребра  4  м  и   12 м,  а  каждое  из  остальных ребер равно 7 м.

2369.   Гранями параллелепипеда служат ромбы, диагонали которых равны 3 см и 4 см. В параллелепипеде имеются трехгранные  углы,   составленные  тремя  острыми   углами  ромбов. Найти объем параллелепипеда.

2370.   Найти объем треугольной пирамиды, стороны основания которой  равны  а, b и  с, если каждая из этих сторон равна боковому ребру, не пересекающемуся с ней.

2371.  Основание  пирамиды  SABCD  есть  трапеция  с параллельными сторонами   АВ  и  CD. Доказать, что объем пирамиды равен  ⁴/₃  произведения площади треугольника MSN, где MN есть средняя линия трапеции, на расстояние ребра АВ от плоскости.

2372.  Многогранник имеет следующее строение: две его грани (основания)  являются  многоугольниками, расположенными в параллельных плоскостях; остальные грани (боковые) представляют собой  трапеции,   параллелограммы или треугольники, у которых каждая вершина является одновременно вершиной одного из оснований. Доказать, что объем такого многогранника равен  ¹/₆ H(S₁+ S₂ + 4S₃),   где   Н — расстояние   между    плоскостями   основания, S₁ и S₂ — площади основания, a S₃ есть  площадь  сечения, равноотстоящего от обоих оснований.

2373.  Тело ограничено сверху и снизу двумя   прямоугольниками со сторонами, равными a, b и a₁ b₁.  Стороны прямоугольников  соответственно   параллельны.   С   боков    тело  ограничено трапециями. Расстояние между параллельными плоскостями прямоугольных оснований равно h. Найти объем тела.

2374.  Диагонали двух  одинаковых  кубов  с  ребром,   равным a, лежат на одной и той же прямой. Вершина второго куба совпадает с центром первого, и второй куб повернут вокруг диагонали на 60° по отношению к первому. Найти объем общей части этих кубов.

2375.  Около шара описан усеченный конус, площадь нижнего основания которого в а раз больше площади его верхнего  основания. Во сколько раз объем усеченного  конуса  больше объема шара?

2376.   В конус вписан шар. Доказать, что  отношение полной поверхности    конуса   к   поверхности    шара    равно   отношению их объемов.

2377.   Высота цилиндра равна радиусу его основания и имеет длину а. Через ось цилиндра проведена  другая  цилиндрическая поверхность, делящая окружность основания на две дуги, длины которых относятся, как 2:1. Эта цилиндрическая поверхность делит данный цилиндр на две части.   Найти  боковую  поверхность и объем большей части цилиндра.

2378.  Отношение высоты конуса к радиусу описанного  около него шара  равно q.   Найти  отношение  объемов  этих  тел.   При каких значениях q задача не имеет решения?

2379.   В шар радиуса R вписана правильная четырехугольная пирамида, основание  которой делит  перпендикулярный  к  нему радиус    пополам.    Определить    поверхность   шара,   вписанного в пирамиду.

2380.   Конус лежит на плоскости и катится по ней, вращаясь вокруг своей неподвижной вершины. Высота конуса и его образующая равны h и l . Вычислить площадь поверхности, описываемой высотой конуса.

ОТВЕТЫ