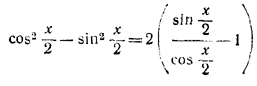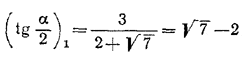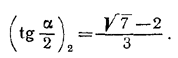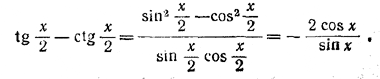|
|
|
|
|
ГЛАВА 2 ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ Ответы и решения 141. Уравнение можно записать так: 4 sin х cos x (sin2 х — cos2 x) = 1 или — 2 sin 2x cos 2x = — sin 4x = l Ответ: x = — π/8 + k • π/2 (k =0, ± 1, ± 2, . . .). ________________________________________________ 142. Уравнение теряет смысл при x = π/2+ kπ и x = — π/4 + kπ , а при прочих x оно равносильно следующему:
После простых преобразований получаем sin х (3 + sin 2х + cos 2х) = 0. Уравнение sin 2х + cos2х + 3 = 0, очевидно, не имеет решений, поэтому исходное уравнение сводится к уравнению sin х = 0. Ответ x = kπ ________________________________________________ 143. Уравнение можно записать в следующем виде: (sin х + cos x)2 + (sin x + cos x) + (cos2 x — sin2 x) = 0 или (sin x+cos x)( l + 2cos x) = 0. Приравнивая каждую из скобок нулю, находим все корни. Ответ: x1 = — π/4+ kπ, x2 = ± 2π/3 + 2kπ. ________________________________________________ 144. Перепишем данное уравнение следующим образом: sin x + 1 — cos 2x = cos x—cos 3x +sin 2x. После понятных преобразований получаем sin x + 2 sin2 x = 2 sin 2x • sin x + sin 2x и, следовательно, sin x (1+2 sin x) (1— 2cos x) = 0. Ответ: x1 = kπ, x2 = π/6( — 1)k+1 + kπ, x3= ± π/3+ 2kπ. ________________________________________________ 145. Перепишем уравнение в виде (1/2sin 2x +√3/2cos2x)2 — 1/4cos(2x — π/6) — 5/4 = 0 или 4cos2(2x — π/6) — cos (2x — π/6) —5 = 0. (1) Решая квадратное уравнение (1), находим cos (2x — π/6) = — 1, x = 7π/12 + kπ. Второй корень квадратного уравнения (1), равный 5/4 , не дает решений, так как |cos α| < l. ________________________________________________ 146. Разделив обе части уравнения на 2, приведем его к виду sin 17x + sin ( 5x + π/3 ) = 0, откуда 2sin (11x + π/6 ) cos (6x — π/6 ) = 0. Ответ: x1 = — π/66 + kπ/11 , х2 = π/36 + (2k + 1)π/12 ________________________________________________ 147. Данное уравнение теряет смысл, когда cos x = 0; поэтому можно считать, что cos x =/= 0. Заметив, что правая часть уравнения равна 3 sin x cos x + 3 cos2 x, и разделив обе части на cos2 x, получим tg2 x (tgx + l ) = 3(tg x + l ), или (tg2 x — 3)( tg x + l ) = 0 Ответ: x1 = — π/4 + kπ, x2 = π/3 + kπ, x3 = — π/3 + kπ ________________________________________________ 148. Пользуясь формулой для суммы кубов двух чисел, преобразуем левую часть уравнения следующим образом (sin x + cos х) (1 — sin х cos x)= ( 1 — 1/2sin2x ) (sin x + cos x). Исходное уравнение, следовательно, принимает вид ( 1 — 1/2sin2x ) (sin x + cos x—1) = 0. Первая скобка вообще не обращается в нуль. Поэтому достаточно рассмотреть уравнение sin x + cos x — 1 = 0. Последнее приводится к виду sin ( x + π/4 ) = 1/√2 Ответ: x1 =2πk, x2 = π/2 + 2πk. ________________________________________________ 149. Пользуясь известными формулами, запишем уравнение в следующем виде cosec2 x — sec2 x—ctg2 x — tg2 x — соs2 x — sin2 x = —3. (1) Так как cosec2 x = 1 +ctg2 x, sec2 x — 1 + tg2 x, то уравнение (1) приводится к виду tg2 x = l. Ответ: x = π/4 + k π/2. ________________________________________________ sin4 x/3 + cos4 x/3 = ( sin2 x/3 + cos2 x/3) — 2 sin2 x/3 cos2 x/3 = 1 — 1/2 sin2 2/3 x преобразуем уравнение к виду sin2 2x/3 = 3/4. Ответ: х = (3n ± 1)/2 π (п = 0, ± 1, ± 2, . . .). ________________________________________________ 151. Используя тождество, содержащееся в решении предыдущей задачи, получим уравнение sin22х+ sin 2х— 1=0. Решая его, находим sin 2х = (√5 — 1)/2 Ответ: х = ( — l)k 1/2 arcsin(√5 — 1)/2+ kπ/2 ________________________________________________ 152. Запишем данное уравнение в виде (1 +k) cos x cos (2x — α) = cos (x — α) + k cos 2x cos (x — α). (1) Так как cos x cos (2x — α) = 1/2 [cos (3x—α) + cos (x — α)], cos (x—α) cos 2x = 1/2 [cos (3x—α) + cos (x + α)], то уравнение (1) примет вид k [cos (x — α) — cos (x + α)] = cos (x—α) — cos(3x — α) или k sin x sin α = sin (2x — α)sin x, (2) Уравнение (2) распадается на два: а) sin x = 0; тогда x = lπ; б) sin (2x — α) = k sin α; тогда x = α/2+ (— 1)n • 1/2 arcsin ( k sin α) + π/2 n Для того чтобы последнее выражение имело смысл, k и α должны быть связаны условием | k sin α | < 1. ________________________________________________ 153. Так как числа а, b, с, d являются последовательными членами арифметической прогрессии, то можно положить b = а + r, с = а + 2r, d = a + 3r (r — разность прогрессии). Пользуясь формулой sin α sin β = 1/2 [cos (α — β ) — cos (α + β )], представим уравнение в виде cos (2а + r) х—cos (2a + 5r) x = 0 или sin (2a + 3r) • sin 2rx = 0, откуда
Написанные формулы имеют смысл, так как 2a + 3r = b + с > 0 и r =/= 0. ________________________________________________ 154. Уравнение запишем в следующем виде
или, после несложных преобразований, в виде (cos x/2— sin x/2) (3cos2 x/2 + 2 sin2 x/2+ sin x/2cos x/2) = 0. Уравнение 3cos2 x/2 + 2 sin2 x/2+ sin x/2cos x/2 = 0 равносильно следующему: 2 tg2 x/2 + tg x/2 + 3 = 0 и не имеет вещественных решений. Ответ: x = π/2 + 2kπ. ________________________________________________ 155. Первое решение. Уравнение теряет смысл при x = kπ, а при прочих х оно равносильно следующему: cos х — sin x = 2 sin 2x • sin x. (1) Заменяя произведение, стоящее в правой части (1), на сумму, по формуле (13) , получаем cos х — sin x = cos x — cos 3x, sin x = cos 3x, откуда sin x = sin ( π/2 — 3x ) и, следовательно, 2 sin (2x — π/4) cos (x — π/4) = 0 Ответ: x1 = π/8 + kπ/2 (2) x2= 3π/4 + kπ. Второе решение. Применяя формулу (20), и полагая tg x = t, получаем уравнение t3 + t2 + t — 1= 0. Разлагая левую часть на множители, получаем (t + 1)( t + l —√2 )( t + l + √2 ) = 0, откуда (tgx)1 = — l, (tgx)2 =√2— 1, (tgx)3 = — l — √2. Ответ: x1 = 3π/4 + kπ; x2 = arctg (√2— 1) + kπ, x3= — arctg (1+√2) + kπ. Замечание: Две последние серии решений можно записать одной формулой (2). ________________________________________________ 156. Применяя к левой части уравнения формулу (14), получаем cos (2x — β) + cos β = cos β откуда cos(2x — β) = 0. Следовательно, x = ± π/4+ kπ + l. и tg x = tg (β/2 ± π/4). ________________________________________________ 157. Исходное уравнение можно записать в виде sin α + [ sin (2φ + α) — sin (2φ — α)] = sin (φ + α) — sin (φ — α), или, после простых преобразований, в виде sin α + 2 sin α cos 2φ = 2 sin α • cos φ. Предполагая sin α =/= 0 (в противном случае cos φ не определяется), получаем l +2 cos 2φ — 2 cos φ = 0, 4 cos2 φ —2 cos φ — 1= 0,
Так как угол φ лежит в третьей четверти, то cos φ < 0. Следовательно,
________________________________________________ 158. Применив формулу cos2(α+x) + cos2 (α—x) = 2a—2 или cos 2α cos 2x = a — 1, откуда
Так как, с другой стороны,
то из (1) находим
Из формулы (1) следует, что задача имеет решения лишь при условии, что |cos2α| > | a —1|. ________________________________________________ 159. Используя формулы (18) и (19), стр. 82, приведем данное соотношение sin α + cos α = √7/2 к виду (2 + √7 )tg2 α/2 —4 tg α/2 — (2 — √7) = 0. Разрешая это уравнение относительно tg α/2, получим
Проверим, удовлетворяют ли найденные значения tg α/2 условиям задачи. Так как 0 < α/2 < π/8 , то 0 < tg α/2 < tg π/8 = √2—1. Значение
Корень √7 —2 следует отбросить, ибо √7 —2 > √2—1. ________________________________________________ 160. Положив sin x — cos x = t и используя тождество (sin x — cos x)2 = l —2 sin x cos x, запишем исходное уравнение в виде t2 + 12t —13 = 0. Это уравнение имеет корни t1 = —13, t2 = 1. Но t = sin x — cos x = √2 sin (х — π/4 ) , откуда | t | < √2, следовательно, корень t1 = —13 можно не рассматривать. Поэтому исходное уравнение сводится к следующему: sin (х — π/4 ) = 1/√2 Ответ: x1 = π + 2kπ, x2 = π/2 + 2kπ. ________________________________________________ 161. Данное уравнение преобразуем к виду 2cos2 x/2 (2+ sin x) + sin x = 0. Используя формулу 2cos2 x/2 = 1 + cos x и раскрывая скобки, получаем 2 + 2 (sin x + cos x) + sin x • cos x = 0. (1) Это уравнение того же типа, что и в задаче 160. Подстановкой sin x + cos x = t уравнение (1) сводится к квадратному уравнению t2 + 4t + 3 = 0, имеющему корни t1 = —1, t2 = —3. Так как | sin x + cos x | < √2 , то исходному уравнению могут удовлетворять лишь корни уравнения sin x + cos x = —1. (2) Решая уравнение (2), получаем x1 = — π/2 + 2kπ, x2 = (2k+1)π. Вторую серию корней следует отбросить, ибо sin x2 = 0 и исходное уравнение теряет смысл. Ответ: х = — π/2 + 2kπ. ________________________________________________ 162. Данное уравнение теряет смысл при x = kπ, а при x =/= kπ может быть записано в виде cos3 x + cos2 x = sin3 x + sin2 x. Перенося все члены уравнения налево и разлагая на множители, получаем (cos х— sin х) (sin2 х + cos2 х + sin х cos х + sin х + cos х) = 0. Отсюда вытекают две возможности: а) sin х — cos х = 0, тогда x1 = π/4 + kπ; (1) б) sin2 х + cos2 х + sin х cos х + sin х + cos х = 0. (2) Уравнение (2) аналогично рассмотренному в задаче 160 и имеет решения x2 = — π/2 + 2kπ (3) и x3 = (2k+1)π (4) Но значения х, содержащиеся в формуле (4), не являются корнями исходного уравнения, так как при х = nπ исходное уравнение теряет смысл. Следовательно, уравнение имеет корни, определяемые формулами (1) и (3). ________________________________________________ 163. Запишем уравнение следующим образом
Приводя дроби к общему знаменателю и отбрасывая его, получим уравнение 2(sin3x cos 2x — cos 3x sin2x) cos 2x = sin 2x (sin 2x sin 3x + cos 2x cos 3x). Но выранжние, стоящее в скобке слева, равно sin x, а стоящее в скобке справа равно cos х. Поэтому мы приходим к уравнению 2 sin х (cos 2х — cos2 х) = — 2 sin3 х = 0, откуда x = kπ. ________________________________________________ 164. Данное уравнение можно записать в виде
или
Заметим, что это уравнение имеет смысл, если sin 2х =/= 0, sin х =/= 0, cos 2х =/= 0. Для тех х, при которых уравнение (1) имеет смысл, 3 sin х cos 2x = sin 3x, или sin x (3 — 4 sin2 x — 3cos2x) = 0, или 2sin3 x = 0. Так как последнее уравнение равносильно уравнению sin x = 0, то ввиду сделанного выше замечания исходное уравнение решений не имеет. ________________________________________________ 165. Уравнение записываем в виде 6 (tg x + ctg 3x) = tg 2x + ctg 3x после чего преобразуем следующим образом:
или
6 cos2 2x = cos2 x 12 cos2 2x — cos 2x — 1 = 0. Решив последнее уравнение, найдем
откуда l) cos 2x = 1/3 x = ± 1/2 arccos1/3+ kπ; 2) cos 2x = — 1/4 , x =± 1/2 arccos ( — 1/4 ) + kπ. В процессе решения было произведено умножение обеих частей уравнения на cos х cos 2х sin 3х. Но легко видеть, что ни при одном из найденных значений х это произведение не обращается в нуль. Следовательно, все найденные значения для х являются корнями исходного уравнения. ________________________________________________ 166. Приведя к общему знаменателю дроби, стоящие в правой части уравнения, и применив формулу a5 — b5 = (a — b)(а4 + а3b + а2b2 + аb3 + b4), получим sin х cos х (sin х — cos х) (sin4 х + sin3 х cos х + sin2 х cos2 х + sin х cos3 х + cos4 х) = = sin x — cos x. Отсюда следует, что либо sin x — cos x = 0, (1) либо sin х cos х (sin4 х + sin3 х cos х + sin х cos3 х + cos4 х + sin2 х cos2 х) —1= 0. (2) Преобразуем теперь уравнение (2), пользуясь тем, что sin4 х + cos4 х = (sin2 х + cos2 х)2 — 2 sin2 х cos2 х, а sin3 х cos х + sin х cos3 х = sin x cos x. Положив еще в уравнении (2) sin x cos x = у, запишем уравнение (2) в виде у3 — у2 — у + 1= 0 (3) или (после разложения левой части на множители) в виде (у —1)2(у +1) = 0. Если у = 1, т. е. sin x cos x = 1, то sin 2x = 2, что невозможно. Если же у = —1, то sin 2x = — 2, что также невозможно. Итак, уравнение (2) не имеет корней. Следовательно, корни исходного уравнения суть корни уравнения (1), т. е. x = π/4 + πn. ________________________________________________ |
|
167. Правая часть уравнения теряет смысл при x = kπ и при x = π/2 + mπ, так как при x = 2lπ не определена функция ctg x/2 , при х = (2l + 1)π не определена функция tg x/2, а при x = π/2 + mπ знаменатель правой части обращается в нуль. При x =/= kπ имеем:
Следовательно, при x =/= kπ и x =/= π/2 + mπ ( k, m —любые целые числа) правая часть уравнения равна —2 sin x cos x. Левая часть уравнения не имеет смысла при x = π/2 + kπ и x = π/4 + l π/2 ( l = = 0, ±1, +2, ...), а при прочих значениях равна —tg х, так как tg (x —π/4) tg (x + π/4) = tg (x —π/4) ctg [ π/2— (x + π/4)] = —tg (x —π/4) ctg (x —π/4)= — 1. Итак, если x =/= kπ, x =/= π/2 + mπ и x =/= π/4 + l π/2 то исходное уравнение имеет вид tg х = 2 sin х cos х. Это уравнение имеет корни x = kπ и x = π/4 + l π/2 . Отсюда следует, что исходное уравнение не имеет корней. ________________________________________________ |