|
|
|
|
|
ГЛАВА 3 ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Ответы и решения |
|
235. Имеем arctg (х2 — 3х — 3) = π/4 , откуда х2 — 3х — 3 = tg π/4 т. е. х2 — 3х — 3 =1. Отсюда находим x1 = 4; x2 =—1. Отв. x1 = 4; x2 =—1. Замечание. Если бы вместо уравнения arctg (х2 — 3х — 3) = π/4 мы имели уравнение arctg (х2 — 3х — 3) = —3π/4, то такое ураанение не имело бы решений, так как главное значение арктангенса не может равняться —3π/4. Если не обратить внимания на это обстоятельство, можно получить то же уравнение х2 — 3х — 3=1, но корни последнего уравнения не годятся. ________________________________________________ arcsin (х2 — 6х + 8,5) = π/6, откуда х2 — 6х + 8,5 = 0,5. Отв. x1 = 4; x2 = 2. ________________________________________________ 237. Взяв тангенсы обеих частей уравнения и учитывая, что tg (arctg α) = α, получим
откуда x1 = —1; x2 = —2. Проверяем эти корни. Если x1=—1, то arctg (х + 2) = arctg 1 = π/4 и arctg(x + 1) =arctg 0 = 0, так что данное уравнение удовлетворяется. Так же докажем, что и второй корень годится. Отв. x1 = —1; x2 = —2. Замечание. Почему проверка необходима, видно из следующего примера. Рассмотрим уравнение arctg (х + 2) — arctg(x + 1) = — 3π/4 отличающееся от данного только значением свободного члена. Заранее нельзя сказать, что оно не имеет решений (ср. задачу 235). Если бы, скажем, arctg (х + 2) равнялся — π/3, a arctg(x + 1) был равен 5π/12 (эти значения могут быть главными значениями арктангенса), то левая часть равнялась бы 3π/4. Взяв тангенсы обеих частей рассматриваемого уравнения, мы снова получим уравнение
но теперь ни один из корней x1 = —1; x2 = —2 не годится. См. еще замечание к задаче 240. ________________________________________________ 238. Берем тангенс обеих частей уравнения. Предварительно находим (см. предыдущую задачу):
и тогда получаем
Корень этого уравнения есть х = 1/7 его нужно проверить (см. замечание к предыдущей задаче). Подставляя в левую часть уравнения х = 1/7 , получаем 2 arctg 1/7 — arctg 1/7. Угол α = arctg 1/2 заключен в пределах между 0 и π/4 (так как tg α = 1/2 < 1). В тех же пределах лежит угол β = arctg 1/7 . Угол 2α принадлежит первой четверти, а угол 2α— β лежит между —π/4 и π/2 Но tg (2α— β) = 1, так что 2α— β = πn + π/4. Но только при n = 0 угол 2α— β попадает внутрь найденных нами границ. Следовательно, данное уравнение удовлетворится. Отв. х = 1/7. ________________________________________________ 239. Возьмем синусы от обеих частей равенства. Можно положить
(см. решение задачи 221); но можно обойтись без них, воспользовавшись формулой sin(arcsin x) = х (она непосредственно вытекает из определения арксинуса) и формулой cos(arcsin x) = √1 — x2 1) 1) Эта формула выводится следующим образом. Положим arc sin х = α. Тогда sin α = х и cos α = √1 — x2 . Перед радикалом берется только знак плюс, так как угол α = arcsin x лежит в границах от —90° до +90° (главное значение арксинуса!). Подставляя вместо α выражение arcsin x, получаем требуемую формулу. Следовательно, синус левой части равен
и данное уравнение принимает вид
Решив его, находим х = 2/3 . Этот корень нужно проверить (см. замечание к задаче 237), т. е. нужно доказать тождество
Доказательство ведется, как в задаче 223. Oтв. х = 2/3 ________________________________________________ 240. Взяв тангенсы обеих частей уравнения, получим
откуда х = 1. Это значение надо проверить (см. замечание к задаче 237). Подставляя х = 1 в данное уравнение, получаем
Введем обозначение arctg a/b = φ. (2) Здесь угол φ(главное значение арктангенса) заключен в границах —90° < φ < 90°. (3) При этом обозначении имеем
так что надо проверить равенство φ — arctg tg (φ — 45°) = 45°. (5) Этогравенство будет верным в том и только в том случае, когда arctg tg (φ — 45°) = φ — 45° (6) Равенство же (6) имеет место, когда угол φ — 45° (главное значение арктангенса) заключен в границах —90° < φ — 45° < 90°, (7) т. е. когда —45°< φ < 135°, (8) Учитывая неравенство (3), получаем для угла φ более тесные пределы —45°< φ < 90°. (9) Из (2) и (9) находим a/b = tg φ > tg (—45° ) т. е. a/b > — 1 . (10) Обратно, при a/b > — 1 угол φудовлетворяет неравенству (9). Следовательно, данное уравнение имеет решение (х = 1) при a/b > — 1. При a/b < — 1 решений нет. Например, при а = — √3 , b = 1 имеем arctg a/b = arctg (— √3) = — 60°;
так что левая часть данного уравнения равна —135°, а правая часть при х = 1равна 45°. Отв. х =1 при a/b > — 1; уравнение не имеет решения при a/b < — 1 . ________________________________________________ |
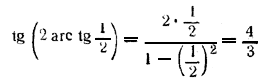
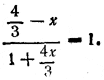
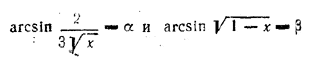
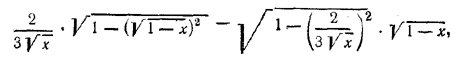
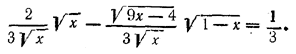

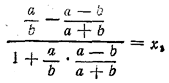
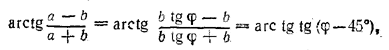 (4)
(4)