|
241. Неравенство равносильно следующему
sin2 x + sin x — 1 > 0. (1)
Разложив квадратный трехчлен, стоящий в левой части (1), на множители, получим
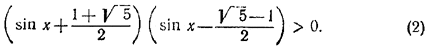
Но 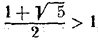 и поэтому и поэтому 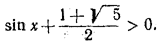 . Следовательно, исходное неравенство равносильно следующему: . Следовательно, исходное неравенство равносильно следующему: 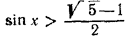 и имеет решения и имеет решения
2kπ + φ < х < π — φ + 2kπ,
где 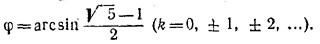
________________________________________________
242. Исследуемое выражение не имеет смысла при х = π/2 + πп.
При прочих значениях х умножим обе части неравенства на cos2 x. Получим равносильное неравенство
(sin 2x)2 + 3/2 sin 2x — 2 > 0.
Решив полученное квадратное неравенство, найдем, что либо
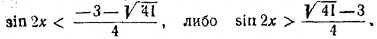
Первое из этих неравенств не может выполняться. Следовательно,
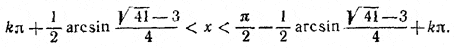
________________________________________________
243. Преобразуя произведение синусов в сумму, заменим данное неравенство следующим равносильным
cos 3х > cos 7х или sin 5х sin 2х > 0.
Но при 0 < х < π/2 имеем sin 2x > 0 и, следовательно, исходное неравенство равносильно следующему: sin 5х > 0.
Ответ: 0 < х < π/5 и 2/5π < х < π/2
________________________________________________
244. Выражение, стоящее в знаменателе левой части неравенства, положительно, так как | sin x + cos х | = | √2 sin ( x + π/4 ) | < √2 .
Поэтому неравенство равносильно следующему:
sin2 х > 1/4 или | sin х | > 1/2 ,
Ответ: π/6 + kπ < х < 5/6π + kπ.
________________________________________________
245. Запишем неравенство в виде
(cos х — sin x) [ 1 — (cos x + sin х)] = 2 sin x/2 ( sin x/2— cos x/2 ) (cos x — sin x) > 0. (1)
Ho sin x/2 > 0, так как 0 < х < 2π. Рассмотрим два возможных случая, при которых выполняется неравенство (1)
Случай 1.
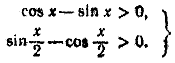 (2) (2)
По условию 0 < х < 2π. Учитывая это, из (2) находим, что первое неравенство выполняется при 0 < х < π/4 или 5/4π < х < 2π, второе—при π/2 < х < 2π. Следовательно, в этом случае 5/4π < х < 2π.
Случай 2.
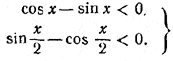 (3) (3)
Система (3) с учетом того, что 0 < х < 2π, удовлетворяется при π/4 < х < π/2
Ответ:
π/4 < х < π/2 и 5/4π < х < 2π
________________________________________________
246. Положим tg x/2 = t. Тогда неравенство примет вид
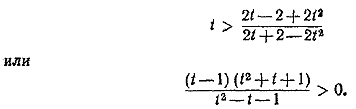 ( 1 ) ( 1 )
Так как t2 + t + 1 > 0 при всех действительных значениях t, то неравенство (1) равносильно неравенству
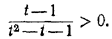 (2) (2)
Трехчлен t2 — t — 1 имеет корни 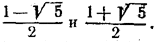 Решив (2), найдем, что Решив (2), найдем, что
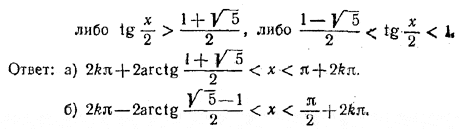
________________________________________________
247. Из формул для sin 3x и cos 3x находим:
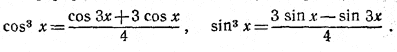
Пользуясь этими формулами, запишем данное неравенство в виде
(cos 3х + 3 cos х) соs 3х — (3 sin х —sin 3х) sin 3х > 5/2
или
sin2 3x + cos2 3x + 3 (cos 3x cos x — sin 3x sin x) > 5/2,
или
cos 4x > 1/2
откуда — π/3 + 2πп < 4х < π/3 + 2πп,
или
— π/12 + 1/2πп < х < π/12 + 1/2πп (n = 0, ± 1, ±2, ....).
________________________________________________
248. Неравенство, которое нужно доказать, можно записать в виде
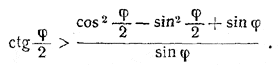 (1) (1)
Но sin φ > 0 при 0 < φ < π/2 , поэтому, после умножения обеих частей неравенства (1) на sin φ , получим равносильное неравенство
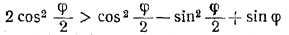
или 1 > sin φ. Последнее неравенство при 0 < φ < π/2 выполняется; следовательно, справедливо и исходное неравенство.
________________________________________________
249. Положив tg x = t , получим:
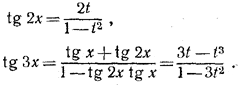
Левая часть теряет смысл для тех значений х, при которых t2 =1, t2 = 1/3. При прочих значениях х левая часть неравенства равна t4 + 2t2 + 1 и, следовательно, принимает положительные значения.
________________________________________________
250. В силу того что
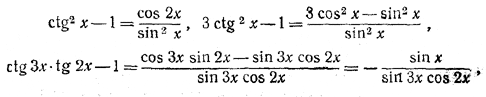
левая часть неравенства может быть записана в виде
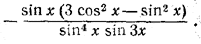
Но
sin 3x = sin (x + 2x) = sin x cos 2x + cos x sin 2x = sin x (3 cos2 x— sin2 x),
поэтому заданное неравенство сводится к очевидному неравенству
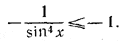
________________________________________________
251. Используя формулу 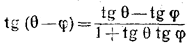 и условие tg θ = n tg φ, получим: и условие tg θ = n tg φ, получим:
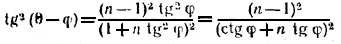
Нужно доказать, что
(ctg φ + n tg φ)2 > 4п или (1 + n tg 2φ)2 > 4n tg 2φ.
Приходим, таким образом, к очевидному неравенству
(1 — n tg 2φ)2 > 0.
________________________________________________
252. Данное неравенство можно записать в виде
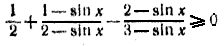
и, умножая на 2(2 — sin х)(3 — sin х) > 0, заменить следующим равносильным:
sin2 х—5 sin х + 4 > 0
или
(4 — sin х ) (1 — sin х ) > 0. (1)
Из (1) заключаем, что последнее неравенство, а вместе с ним и исходное, выполняется при всех х, причем равенство достигается при х = π/2 + 2kπ.
________________________________________________
253. Установим сначала, что
| sin х | < | х |.
Рассмотрим тригонометрический круг радиуса 1 и предположим, что х обозначает радианную меру некоторого положительного или отрицательного угла АОМ (рис. 249).
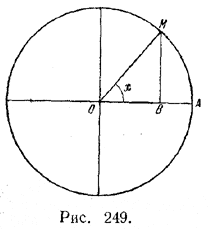
При любом положении точки М
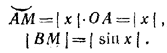
Так как 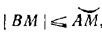 , то | sin х | < | х | (равенство имеем лишь при х = 0). После этого заключаем, что, если 0 < φ < π/2 , т. е. если 0 < cos φ < l < π/2 , то sin cos φ < cos φ. Ho 0 < sin φ < φ < π/2 и поэтому cos φ < cos sin φ. , то | sin х | < | х | (равенство имеем лишь при х = 0). После этого заключаем, что, если 0 < φ < π/2 , т. е. если 0 < cos φ < l < π/2 , то sin cos φ < cos φ. Ho 0 < sin φ < φ < π/2 и поэтому cos φ < cos sin φ.
Окончательно имеем cos sin φ > cos φ > sin cos φ.
Неравенство доказано.
________________________________________________
254. Воспользуемся методом полной индукции. Пусть n = 2, тогда 0 < α < π/4.
Следовательно,
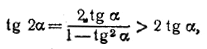
так как 0 < 1— tg2 α < 1. Пусть
tg nα > n tg α (1)
при условии
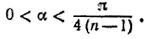 (2) (2)
Докажем, что tg (n + 1) α > (n + 1) tg α , если 0 < α < π/4n.
Применим формулу
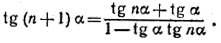 (3) (3)
Так как неравенство (1) выполняется при условии (2), то оно тем более будет иметь место при 0 < α < π/4n.
Но
0 < tg α < l , (4)
и так как 0 < nα < π/4, то
0 < tg nα < 1. (5)
Из (4) и (5) получим:
0 < 1— tg α tg nα < 1. (6)
Из (6) и (3) следует tg (n + 1) α > (n + 1) tg α, что и требовалось доказать.
________________________________________________
255. Так как большему углу первой четверти соответствует большее значение тангенса, то
tg α1 < tg αi < tg αn (1)
для i = 1, 2, ... , n .
Кроме того, cos αi > 0 (i = 1, 2, ... , n). Поэтому неравенства (1) можно записать в виде
tg α1 cos αi < sin αi < tg αn cos αi. (2)
Будем в неравенстве (2) придавать i значения 1, 2, ... , п и сложим все полученные неравенства. Находим:
tg α1 (cos α1 + ... + cos αn) < sin α1 + ... + sin αn < tg αn (cos α1 + ... + cos αn). (3)
Разделив все части неравенства (3) на cos α1 + ... + cos αn (что возможно, так как cos α1 + ... + cos αn > 0), будем иметь:
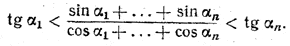
________________________________________________
256. Обозначим левую часть рассматриваемого неравенства через t. Тогда
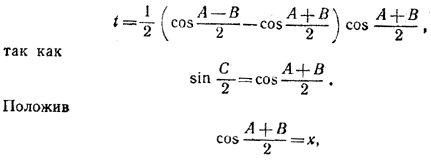
после очевидных преобразований получим:
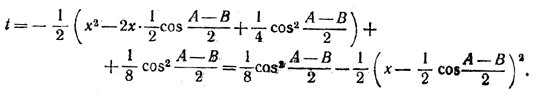
Следовательно,
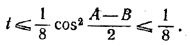
________________________________________________
257. Преобразуем левую часть данного неравенства следующим образом:
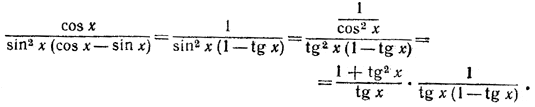
Для сокращения записи положим tg x = t. Так как 0 < х < π/4, то
0 < t < 1. (1)
Таким образом, задача сводится к доказательству неравенства
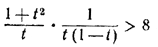
при условии 0 < t < 1.
Но в силу неравенства a2 + b2 > 2 | ab |, имеем 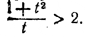
Кроме того, 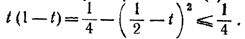
Следовательно, 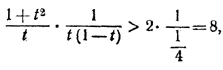 , что и требовалось доказать. , что и требовалось доказать.
________________________________________________
|