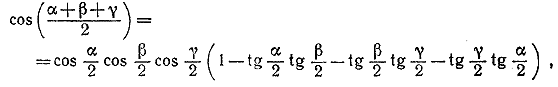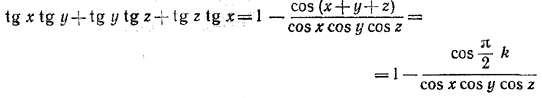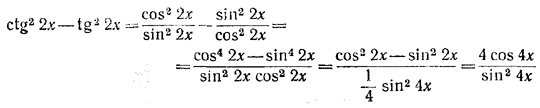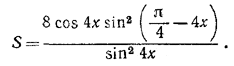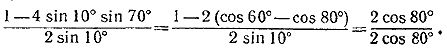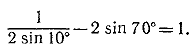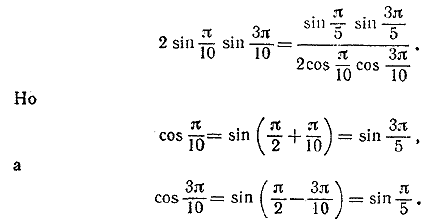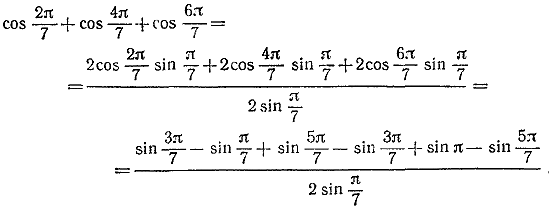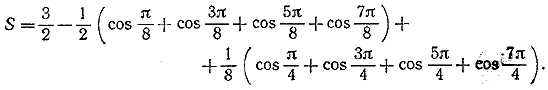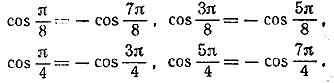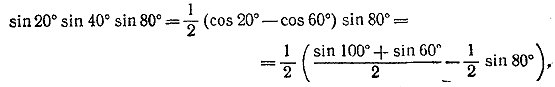|
|
|
ГЛАВА 1 |
|
ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Ответы и решения а3 + b3 = (а+ b)(а2—аb + b2) = (а + b)[(а+b)2 — 3аb], получим sin6 х + cos6 х = (sin2 х + cos2 х) [(sin2х + cos2 х)2 — 3 sin2 х cos2 х] = = l —3 sin2 х cos2 х = l — 3/4 sin2 х. ________________________________________________ 51. Обозначим левую часть тождества через S и заменим произведение 2cos α cos β по формуле (14) суммой cos(α + β )+cos (α — β). Тогда S запишется в следующем виде S = cos2 α — cos(α + β )cos (α — β). Применяя снова формулу (14), находим cos(α + β )cos (α — β) = 1/2 (cos 2α + cos 2β). Если теперь заменить cos2 α на
что и требовалось доказать. ________________________________________________
следует, что tg α + tg β = tg (α + β) [1 — tg α tg β], откуда tg α + tg β — tg (α + β)= — tg α tg β tg (α + β). Полагая в последнем равенстве α = х, β = 2х, получаем нужную нам формулу. ________________________________________________
С другой стороны, применив повторно формулу для тангенса суммы двух углов, легко найдем, что
Сравнивая (1) и (2), приходим к решению задачи. Замечание: Формулу (2) можно вывести также из формул (7) и (8) . ________________________________________________ 54. Пользуясь формулами для суммы и разности синусов, представим левую часть тождества в следующем виде
Отсюда, применив формулу для разности косинусов, легко получим, что левая часть тождества совпадает с правой. ________________________________________________ 55. Используя тождество задачи 54, получим
так как
________________________________________________ 56. Используя тождество, указанное в задаче 54, получим sin2nα +sin 2nβ+ sin2nγ = 4 sin n (α + β) sin n (β + γ) sin n (γ + α) (1) Имеем далее sin n (α + β) = sin n (π — γ) = (—1)n+1 sin nγ. Преобразуя аналогично два других множителя в правой части (1), приходим к решению задачи. ________________________________________________ 57. Для доказательства умножаем обе части равенства cos(α + β) = 0 на 2 sin β и применяем формулу (15) . ________________________________________________ 58. Допустимые значения аргументов определяются условием cos α cos cos(α + β) =/= 0. Заметим, что равенство tg(α + β)= 2tgα, (1) подлежащее доказательству, содержит аргументы α + β и α. Естественно поэтому ввести эти же аргументы и в исходное равенство. Имеем β = (α + β) — α, 2α + β = (α + β) + α. Подставляя эти выражения для β и 2α + β в исходное равенство 3sin β = sin (2α + β) (2) и пользуясь формулами для синуса суммы и разности углов, преобразуем (2) к следующему виду sin(α + β) cos α = 2cos (α + β) sin α. (3) Разделив обе части (3) на cos α cos (α + β), получим (1). ________________________________________________ 59. Допустимыми являются все значения α и β, кроме тех, при которых cos(α + β) = 0, cos β = A. Заметив, что sin α = sin (α + β — β), запишем исходное равенство в следующем виде sin (α + β) cos β — cos (α + β) sin β = A sin(α + β). (1) Разделив обе части (1) на cos (α + β) =/= 0, получим tg (α + β) cosβ —sin β = A tg (α + β). Выражая отсюда tg (α + β), придем к требуемому равенству. ________________________________________________ 60. Легко проверить, что в силу условий задачи sin α cos α cos β =/= 0, так как в противном случае мы имели бы | m | < | n | . Поэтому равенство, которое нужно доказать, имеет смысл. Это равенство представляем в виде
откуда
В соотношении (2) заменим тангенсы углов α и α + β через синусы и косинусы, приведем дроби к общему знаменателю и отбросим общий знаменатель. Получим m [cos α sin (α + β) —sin α cos (α + β)] — n [sin α cos(α + β)+cos α sin (α + β)] = 0 (3) или m sin β — n sin (2α + β)=0. (4) Итак, доказательство сводится к доказательству соотношения (4). Так как соотношение (4) выполняется по условию задачи, то имеет место (3), а следовательно, и (2). Но из (2) следует (1), а из (1) следует соотношение
которое и нужно было доказать. ________________________________________________ cos (х + у + z) = cos (х + у) cos z — sin (x + y) sin z = = cos x cos у cos z — cos z sin x sin у —cos у sin x sin z — cos x sin у sin z. Так как по условию задачи cos x cos у cos z =/= 0, то из этого тождества следует, что cos(х + у + z) = cos x cos у cos z (1— tg x tg у — tg у tg z — tg z tg x). ________________________________________________ 62. Первое решение. По условию задачи 0< α < π, 0 < β < π, 0 < γ < π и α + β + γ = π (1) Поэтому из (1) следует, что С другой стороны, по формуле тангенса суммы
Приравнивая празые части равенств (2) и (3) и освобождаясь от знаменателей, получаем требуемое равенство. Второе решение. Из формулы
доказанной в предыдущей задаче, сразу находим, что
так как
________________________________________________ 63. По смыслу рассматриваемого в задаче выражения cos x cos у cos z =/= 0. Поэтому из формулы, полученной в задаче 61, на ходим
Если k нечетно, то исследуемое выражение равно 1 и не зависит от x, у, z. При четном k оно зависит от x, у, z. ________________________________________________ 64. Первое решение. Заметим сначала, что tg β tg γ =/= 1, так как в противном случае мы имели бы tg β + tg γ = 0, что несовместно с равенством tg β tg γ = 1. Поэтому из условия задачи вытекает, что
откуда находим α = kπ — β — γ, т. е. α + β + γ = kπ . Второе решение. В задаче 61 доказана формула для косинуса суммы трех углов. Аналогично можно получить формулу sin (α + β + γ) = cos α cos β cos γ (tg α+tg β + tg γ — tg α tg β tg γ), предполагая, что cos α cos β cos γ =/= 0 Из этой формулы находим, что, и условиях данной задачи, sin (α + β + γ) = 0, т. е. α + β + γ = kπ ________________________________________________ 65. Обозначим данную сумму через S. Первые два слагаемых преобразуем следующим образом
Следовательно,
Так как 1—sin 8x = 2 sin2 ( π/4 — 4x ), то окончательно получаем
________________________________________________ 66. Обозначим рассматриваемое выражение через S. Первые два слагаемые преобразуем по формуле (16) , а произведение cos α cos β заменим суммой по формуле (14) , наконец, заменим sin2 γ на 1—cos2 γ . Тогда получим S = —1/2 (cos 2α+cos 2β) —cos 2γ + [cos(α + β) + cos(α—β)]cos γ. Преобразуя сумму cos 2α+cos 2β в произведение и раскрывая квадратные скобки, получаем S = — cos (α + β) cos (α—β)—cos2 γ + cos (α + β) cos γ + cos(α—β) cos γ Группируя слагаемые в S, находим, что S= — [cos (α—β) — cos γ] [cos (α + β) — cos γ]. Следовательно,
________________________________________________ 67. Исследуемое выражение можно преобразовать так (см. (13) ).
Таким образом,
________________________________________________ 68. В силу формулы (12), левая часть тождества равна 2sin π/10 sin 3π/10 (1) Умножив и разделив (1) на 2 cos π/10cos 3π/10 и пользуясь формулой для sin 2α, получим
Следовательно, левая часть тождества равна 1/2. ________________________________________________ 69. Умножив и разделив левую часть тождества на 2 sin π/7 и пользуясь формулами, выражающими произведения тригонометрических функций через суммы, найдем:
Отсюда следует, что рассматриваемая сумма равна —1/2 ________________________________________________ 70. Применив ко всем слагаемым исследуемой суммы S сначала формулу (16), а затем (17) , найдем, что
Суммы, стоящие в скобках, равны нулю, так как
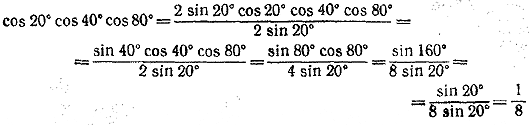
Следовательно, S = 3/2. ________________________________________________ tg α tg(60° — α)tg(60°+α) = tg 3α (1) положить α = 20° (см. задачу 53), то сразу получаем tg 20° tg 40° tg 80° = √3 (2) Приведем другое решение, не использующее формулу (1). Преобразуем отдельно произведения синусов и косинусов. Используя формулы (13) и (15) , получим
Замечая, что sin 100°= sin 80°, Находим Далее,
Итак, cos 20°cos 40°cos 80° = 1/8 (4) Из (3) и (4) следует (2). ________________________________________________ |
|
|
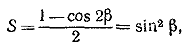
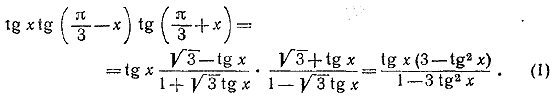
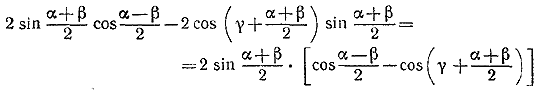
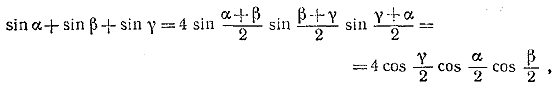
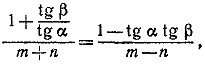
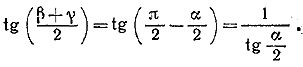 (2)
(2) 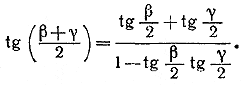 (3)
(3)