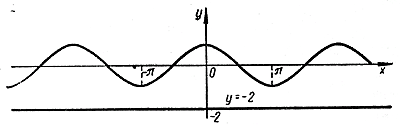
Уравнение cos х = а  

Каждый  корень  уравнения

cos х = а       (1)

можно рассматривать как абсциссу некоторой точки пересечения синусоиды у = cos х с прямой у = а, и, наоборот, абсцисса каждой такой точки пересечения является одним из корней уравнения   (1).Таким образом, множество всех корней уравнения (1) совпадает с множеством абсцисс всех точек пересечения  косинусоиды у = cos х с прямой у = а.

Если  | а | >1 , то косинусоида у = cos х не пересекается с прямой у = а .

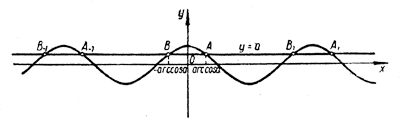
В   этом  случае  уравнение  (1)  не  имеет корней.

При |а| < 1 получается бесконечно много точек пересечения .

для а > 0

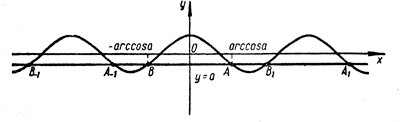
 для а < 0.

Все эти точки пересечения мы разобьем на две группы:

... , A_—2 , A _{— 1} , A  ₁ , A₂ , ...  ,

... , B_—2 , B _{— 1} , B  ₁ , B₂ ,  ...  ,

Точка А имеет абсциссу arccos а, а все остальные точки первой группы отстоят от нее на расстояния, кратные 2π. Поэтому их абсциссы выражаются  как

arccos a + 2kπ.        (2)

Точка В, как легко понять из рисунков, имеет абсциссу    — arccos а,    а все остальные точки второй группы удалены от нее на расстояния, кратные 2π. Поэтому их абсциссы выражаются  как

arccos а + 2nπ.         (3)

Таким образом, уравнение (1) имеет две группы корней, определяемых формулами (2) и (3). Hо эти две формулы можно, очевидно,  записать  в  виде одной  формулы

х =  ± arccos a + 2mπ,          (4)

где m пробегает все целые числа (m = 0, ±1, ±2, ±3, ...).

Те рассуждения, которые мы проводили при выводе этой формулы, верны лишь при
| a | =/= 1. Однако формально соотношение (4) определяет все корни уравнения cos x=a и при |а| =1. (Докажите это!) Поэтому можно сказать,  что формула   (4) дает все корни уравнения (1) при любых  значениях а,  если только  |а| < 1.

Но все же в трех частных случаях (а = 0, а = —1, а = +1) мы рекомендуем не обращаться к формуле (4), а пользоваться другими соотношениями. Полезно запомнить, что корни уравнения cos х = 0 задаются формулой

х = ^π/₂ +nπ;         (5)

корни уравнения cos х = —1  задаются формулой

х = π + 2mπ;         (6)

и, наконец, корни уравнения cos х = 1 задаются формулой

х =  2mπ;              (7)

В заключение отметим, что формулы (4), (5), (6) и (7) верны лишь в предположении, что искомый угол х выражен в радианах. Если же он выражен в градусах, то эти формулы нужно естественным образом изменить. Так, формулу (4) следует заменить формулой

х =  ± arccos a + 360° n,

формулу   (5) формулой

х = 90° + 180° n и т. д.

Примеры.

1)  Решить уравнение

cos 3 х = ¹/₂  .

По  формуле   (4)   находим:

3х = ± arccos ¹/₂ + 2mπ = ± ^π/₃ + 2mπ.

Отсюда

х = ± ^π/₉ + ²/₃ mπ.

Ответ к задаче можно было бы выразить и в градусах:

х = ±20° + 120°m.

Однако не следует записывать ответ в   форме,   в   которой градусы перемешиваются с радианами (например, х = ±20° + ²/₃ mπ  или х = ± ^π/₉+120°m ).

2)   Решить уравнение

cos ( ^π/₄ — 2x)= — 1

Очевидно, что здесь искомый угол х выражен в радианах. Поэтому, используя формулу (6), решение можно записать таким образом:

^π/₄— 2x  = π + 2mπ,

откуда

2x = — ^3π/₄ — 2mπ,

или

x = — ^3π/₈ — mπ,

Поскольку   под m  здесь   подразумевается   любое   целое   число (в том числе и отрицательное), то ответ можно записать в виде

x = — ^3π/₈ + mπ,

Упражнения

Решить уравнения :