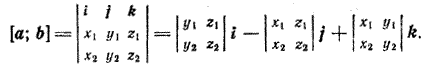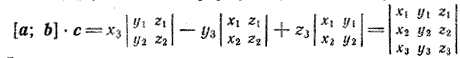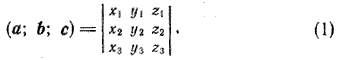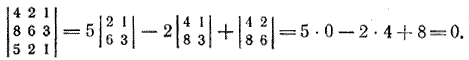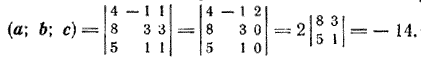Глава I. Векторы на плоскости и в пространстве

§ 24*. Смешанное произведение трех векторов, заданных своими координатами.

Пусть векторы а, b и с заданы своими прямоугольными декартовыми координатами

а = (х₁; у₁; z₁),  b = (х₂; у₂; z₂),   с = (х₃; у₃; z₃).

Для вычисления смешанного произведения (а; b; с) найдем   сначала   векторное  произведение  векторов a и b   (§22, формула (4)):

Умножим теперь скалярно вектор [а; b] на вектор с =  x₃i + y₃j + z₃k. По формуле (2) § 19 получим

Следовательно,

т. е. смешанное произведение трех векторов равно определителю третьего порядка, в первой строке которого стоят координаты первого вектора, во второй — второго и в третьей — координаты третьего вектора.

Теперь теорему 2 из предыдущего параграфа можно сформулировать следующим образом.

Для того чтобы векторы а = (х₁; у₁; z₁),  b = (х₂; у₂; z₂) и  с = (х₃; у₃; z₃). были компланарны, необходимо и достаточно, чтобы

Задача 1. Установить, компланарны ли  векторы а = (4; 2; 1), b = (8; 6; 8) и с = (5; 2; 1). Воспользуемся условием (2):

Следовательно, векторы компланарны.  

Задача 2. Найти объем параллелепипеда, построенного на векторах а = (4; —1; 1), b = (8; 3; 3) и с = (5; 1; 1).

Найдем смешанное произведение данных векторов:

Теперь по теореме 1 § 23 получаем

V = |(a; b; с)| = |—14| = 14 (куб. ед.).