Глава II. Прямые   на   плоскости.

§ 28. Уравнение   прямой,   проходящей   через   две   данные точки

Пусть даны две точки M₁ и М₂ с координатами (x₁; y₁)  и  (x₂; y₂). Чтобы составить уравнение прямой, проходящей через точки M₁ и М₂, примем вектор а = M₁M₂^> за направляющий вектор этой прямой.

Каноническое уравнение прямой (§ 27), проходящей через точку M₁ (x₁; y₁) и имеющей направляющий вектор а = (а₁; а₂), имеет вид

Подставив в это уравнение координаты вектора  а = M₁M₂^> = (x₂ — x₁; y₂ — y₁), получим

             (1)

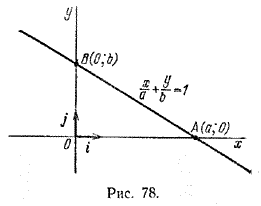
Это уравнение называется уравнением, прямой, проходящей через две точки.

Если в уравнении (1) один из знаменателей обращается в нуль, то для получения уравнения следует приравнять нулю соответствующий числитель.

Например, если x₂ — x₁ = 0, то искомым уравнением будет х — x₁ = 0. В этом случае точки M₁ и М₂ находятся на одинаковом расстоянии от оси Оу и прямая M₁М₂ параллельна этой оси.

Часто бывает нужно составить уравнение прямой, проходящей через две точки, одна из которых лежит на оси Ох, другая на оси Оу.

Пусть на осях координат даны точки А(а; 0) и B(0; b), и пусть а =/= 0, b =/= 0 (рис. 78).

Полагая в формуле (1) x₁ = а, y₁ = 0, x₂ = 0, y₂ = b, получаем

или

       (2)

Это уравнение называется уравнением прямой в отрезках, так как числа а и b указывают, какие отрезки отсекает прямая на осях координат.

Задача 1. Составить уравнение прямой, проходящей через две точки M₁(3; —2) и
М₂(5; 1).

После подстановки координат точек M₁ и М₂ в уравнение (1) получим

или 3х — 2у — 13 = 0.

Задача 2. Вершины треугольника находятся в точках А(—3; 2), B(1; 5) и С(5; —7). Написать уравнение медианы этого треугольника, проходящей через вершину А. Построить треугольник и медиану.

Пусть точка A₁(x₁; у₁) — середина стороны ВС. Для нахождения ее координат воспользуемся формулами деления отрезка пополам (§ 25 формулы (5)):

Положив теперь в формуле (1) x₁ = 3, у₁ = — 1, x₂ = —3, у₂ = 2 получим уравнение прямой АА₁ т. е. искомое уравнение медианы,

    или     x + 2y — 1 = 0.

На рис.    79    изображен   треугольник   ABC и медиана АА₁.

Задача   3. Для    прямой y = ³/₄х — 3  написать ее уравнение в отрезках. Вычислить площадь треугольника, образованного этой прямой и осями координат.

Преобразуем данное уравнение следующим образом:

³/₄х — y = 3 ,   ^x/₄ —  ^y/₃ = 1

В результате получим уравнение      ^x/₄ +  ^y/_—3 = 1 которое и является уравнением данной прямой в отрезках.

Треугольник, образованный данной прямой и осями координат является прямоугольным треугольником с катетами, равными 4 и 3 (рис. 80), поэтому его площадь равна
                                                                     ¹/₂ • 4 • 3 = 6 (кв. ед.).

Задача 4. Составить уравнение прямой, проходящей через точку A (4; —3) так, что площадь треугольника, образованного этой прямой и осями координат, равна 3 кв. ед.

Воспользуемся уравнением прямой в отрезках.      

Пусть  ^x/_a +  ^y/_b = 1  уравнение искомой прямой. Тогда, так как точка А (4; —3) лежит на прямой, то а и b удовлетворяют уравнению

 ⁴/_a —  ³/_b = 1     или     4b — 3а = аb.

Площадь треугольника, образованного этой прямой и осями координат, очевидно, равна   ¹/₂ • | a | • | b |, поэтому а и b удовлетворяют также уравнению

| a | • | b | = 6.

Следовательно, чтобы найти уравнение прямой, достаточно решить систему уравнений

Полученная система уравнений, очевидно, равносильна следующим двум простым системам уравнений:

Из первой системы находим a₁ = 2, b₁ = 3   и   a₂ = — 4, b₂ = —  ³/_{2 .} Вторая система решении не имеет. Итак, задача имеет два решения (рис. 81)

или

3x + 2y — 6 = 0    и    3х + 8у + 12 = 0.