|
|
|
Глава III. Кривые второго порядка § 38. Эллипс. Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости постоянна и больше расстояния между этими точками. Данные точки называются фокусами эллипса, а расстояние между ними — фокальным расстоянием. С эллипсом человеку приходится иметь дело в самых различных областях его деятельности. Садовник размечает клумбу, ограниченную эллипсом. Художник вычерчивает эллиптический контур для росписи стен или потолка зала. Математик рассчитывает эллиптическую траекторию движения спутника Земли. Наконец, сама Земля, как известно, движется по эллипсу, в одном из фокусов которого находится Солнце.
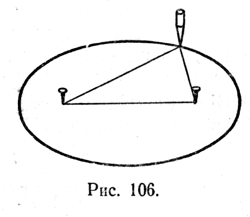
Покажем, как, исходя из определения эллипса, можно разбить эллиптическую клумбу. Забьем в землю два колышка (рис. 106), затем тонкую веревку свяжем в кольцо и наденем веревочное кольцо на оба колышка. Натянув веревку третьим колышком, вычертим им эллипс. Изменяя расстояние между колышками и длину веревки, можно получать эллипсы разных размеров и формы.
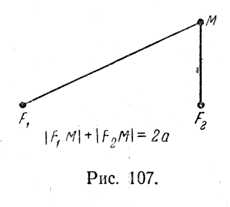
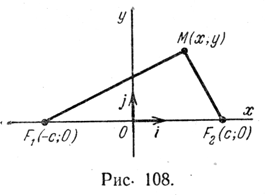
Обозначим фокусы эллипса буквами F1и F2. Пусть фокальное расстояние |F1F2| = 2с. Если М — произвольная точка эллипса (рис. 107), то по определению эллипса сумма |F1M | + |F2M | = 2a. (1) Отметим, что по определению эллипса 2а > 2с, т. е. а > с. Равенство (1) есть уравнение эллипса. Если точка F1 совпадает с точкой F2, то уравнение эллипса принимает вид 2|F1M| = 2a, т. е. |F1M| = a. Это уравнение является уравнением окружности радиуса а с центром в точке F1 Выберем систему координат так, чтобы ось абсцисс проходила через фокусы эллипса; ось ординат проведем через середину отрезка F1F2 перпендикулярно ему. Тогда фокусами будут точки F1(— с; 0) и F2(c; 0) (рис. 108).
Пусть М(х; у) —любая точка эллипса, тогда |F1M|= √(x + c)2 + y2 и |F2M|= √(x — c)2 + y2 . Подставляя найденные значения |F1M| и |F2M| в уравнение (1), получаем √(x + c)2 + y2 + √(x — c)2 + y2 = 2а. (2) Уравнение (2) является уравнением эллипса в выбранной системе координат. Это уравнение можно привести к более простому виду. Для этого сначала перенесем второе слагаемое левой части уравнения в правую часть: √(x + c)2 + y2 = 2а — √(x — c)2 + y2 . (3) Затем возведем обе части полученного равенства в квадрат: (x + c)2 + y2 = 4а2 — 4а √(x — c)2 + y2 + (x — c)2 + y2 . После упрощений получим √(x — c)2 + y2 = а — c/a х. (4) Возводя в квадрат обе части уравнения (4), будем иметь (x — c)2 + y2 = (а — c/a х)2 или х2 — 2сх + c2 + y2 = a2 — 2сх + c2/a2 х2, откуда
По определению эллипса а > с, поэтому a2 — c2 —-положительное число. Обозначим его через b2, т. е. положим b2 = a2 — c2 . Тогда уравнение (5) примет вид
Разделив обе части последнего равенства на b2, получим уравнение
Оно называется каноническим уравнением эллипса. При а = b, т. е. в случае с = 0, уравнение (6) принимает вид х2 + y2 = a2, т. е. является каноническим уравнением окружности. Замечание. Полученное нами уравнение (6) является следствием уравнения (2). Поэтому координаты х и у каждой точки эллипса, заданного уравнением (2), удовлетворяют и уравнению (6). При выводе уравнения (6) мы дважды возводили в квадрат обе части уравнения. Такая операция могла привести к тому, что уравнению (6) удовлетворяли бы не только координаты х и у точек эллипса, но и координаты каких-то точек, не принадлежащих эллипсу (как известно, при возведении в квадрат могут появиться посторонние решения). Покажем, что в данном случае этого не произошло. Поскольку √(x — c)2 + y2 < √(—a — c)2 + b2 = √a2 + 2ac+ c2 + b2 = √2a2 + 2ac < √2a2+2a2 = 2а, а — c/a х > а — c/a a = а — с > 0. Итак, уравнения (2) и (6) равносильны. Задача 1. Написать каноническое уравнение эллипса, проходящего через точку М(5; 0), если фокальное расстояние равно 6. Так как |F1F2| = 6, то с = 3. Запишем каноническое уравнение эллипса:
По условию точка М (5; 0) принадлежит эллипсу, следовательно, 25/ a2= 1. откуда
Задача 2. Доказать, что уравнение 36x2 + 100y2 — 3600 = 0 является уравнением эллипса. Найти координаты фокусов и фокальное расстояние. Разделив обе части уравнения на 3600, получим
Это уравнение является уравнением эллипса. Из равенства a2 — c2 = b2 следует, что c2= a2 — b2. Так как a2= 100 и b2= 36, то c2 = 64, откуда с = 8. |
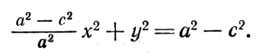 (5)
(5)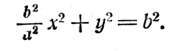 .
.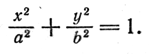 (6)
(6)