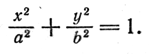Глава III. Кривые второго порядка

§ 44. Общее уравнение второго порядка с двумя переменными.

В главе II мы исследовали общее уравнение первого порядка с двумя переменными, т. е. уравнение вида

Aх + By + С = 0,    A² + В² =/= 0.    (1)

Мы установили, что множеством всех точек плоскости, координаты которых х и у удовлетворяют уравнению (1), является прямая.

Общее уравнение второго порядка с двумя переменными имеет вид

Ах² + Вху + Су² + Dx + Еу + F = 0,      A² + В²  + С² =/= 0.          ( 2)

Возникает естественный вопрос, что представляет собой множество точек плоскости, координаты которых удовлетворяют уравнению (2)? Другими словами, какие множества точек плоскости могут задаваться этим уравнением?

Покажем, что существует 8 различных типов таких множеств.

1) Положив в уравнении (2)

А = ¹/_a2  ,     С =  ¹/_b2 ,    F = — l,    B = D = E = 0,

получим

Итак, уравнение (2) может быть   уравнением   эллипса.

2) Положив в уравнении (2)

А = ¹/_a2  ,     С = —  ¹/_b2 ,    F = — l,    B = D = E = 0,

получим

Следовательно, уравнение (2) может быть уравнением гиперболы.

3) Если в уравнении (2) положить

C = l  ,   D = — 2p,   A = В = E = F = 0,

то получим

у² = 2рх.

Уравнение (2) может быть уравнением параболы.

4) Если в уравнении (2) выбрать коэффициенты следующим образом:

А = а²  ,  C = — b²,   B = D = E = F = 0,

то оно примет вид

а²х² — b²у² = 0.

Так как   а²х² — b²у² = (ах — by) (ах + by),   то это уравнение является уравнением двух прямых:

ах — by = 0   и   ах + by = 0.

Таким образом, уравнением (2)   может задаваться пара пересекающихся прямых.

5) Взяв в уравнении (2)

C = l ,   F = — а²,   A = B = D = E = 0,

получим

у² — а² = 0,

т. е. уравнение двух прямых у = а и у = —а.

Следовательно, уравнение (2) может быть уравнением двух параллельных прямых.

6) Положив в уравнении (2)

С = 1,   A = B = D = E = F = 0,

получим

у² = 0.

Такое уравнение принято считать уравнением пары совпавших прямых, так как из него следует, что у • у = 0 и, приравнивая каждый множитель нулю, получаем у = 0 и у = 0. Итак, уравнением (2) может быть задача пара совпавших прямых.

7) Если в уравнении (2) возьмем

А = а² , С = b²  , B = D = E = F = 0,

то получим

а²х² + b²у² = 0 .

Этому уравнению удовлетворяют координаты только одной точки плоскости, а именно точки (0; 0).

Отсюда следует, что уравнение (2) может задавать точку.

8) Положив в уравнении (2)

А = ¹/_a2  ,     С =  ¹/_b2 ,    F = l,    B = D = E = 0,

получим

Этому уравнению не удовлетворяют координаты ни одной точки плоскости. То же получится и в случае, когда

C = l ,   F = а² =/= 0,   A = B = D = E = 0.

На плоскости нет точек, координаты которых удовлетворяют уравнению

y² + а² = 0.

Таким образом, уравнение (2) может быть уравнением пустого множества.  

Мы показали, что уравнение (2) может быть уравнением 1) эллипса, 2) гиперболы, 3) параболы, 4) пары пересекающихся прямых, 5) пары параллельных прямых, 6) пары совпавших прямых, 7) точки, 8) пустого множества.

Замечательно то, что, кроме восьми перечисленных типов множеств, не существует других множеств, уравнения которых имели бы вид (2). Это вытекает из следующего утверждения, которое мы примем без доказательства.

Пусть множество точек плоскости задается в некоторой системе координат уравнением

Ах² + Вху + Су² + Dx + Еу + F = 0,      A² + В²  + С² =/= 0.  

Тогда всегда можно перейти (с помощью фopмvл (3) § 13) к новой системе координат, в которой это уравнение будет иметь один из следующих девяти видов:

Уравнения 1)—9) называются каноническими.

Множества, определяемые уравнениями 4)—6), состоят из прямых. Прямые изучались в главе II. Множества, определяемые уравнениями 7)—9) (точка и пустое множество), не представляют интереса.

Уравнения 1)—3) определяют эллипс, гиперболу и параболу. Эти кривые имеют большое значение для космонавтики и астрономии, механики и архитектуры. С ними были знакомы еще древние греки. Греческие математики не знали ни метода координат, ни уравнений, тем не менее все свойства эллипса, гиперболы и параболы были им хорошо известны. Они получали и изучали эти кривые как плоские сечения конической поверхности (см. § 77, глава VI). С тех пор эллипс, гиперболу и параболу называют коническими сечениями. Есть у эллипса, гиперболы и параболы и другое общее название. Уравнения этих кривых обязательно содержат по крайней мере одно слагаемое второго порядка х², у² или ху. Поэтому эллипс, гиперболу и параболу называют кривыми второго порядка.

На протяжении всей истории развития науки и техники кривые второго порядка неизменно привлекали к себе внимание многих исследователей и ученых. Это объясняется тем, что эллипс, гипербола и парабола очень часто встречаются в окружающих нас явлениях природы и человеческой деятельности. Приведем лишь некоторые примеры. Камень или снаряд, выпущенный под острым углом к горизонту, летит по кривой, близкой к параболе (форма кривой немного искажается из-за сопротивления воздуха). Для устройства разнообразных прожекторов и антенн используются так называемые «параболические зеркала». На производстве в некоторых механизмах применяются «эллиптические зубчатки». Часто две величины бывают связаны между собой обратно пропорциональной зависимостью (например, давление и объем газа согласно закону Бойля — Мариотта). Графиком такой функциональной зависимости является гипербола.

Особенно большое научное значение кривые второго порядка приобрели после открытий немецкого астронома Иоганна Кеплера (1571 — 1630) и английского физика и математика Исаака Ньютона (1643—1727). Кеплер, наблюдая за видимыми перемещениями планет на небесной сфере, открыл три закона, один из которых устанавливает, что каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Ньютон не только теоретически обосновал законы движения планет, но и доказал, что каждое тело под действием притяжения другого тела может двигаться только либо по эллипсу, либо по параболе, либо по гиперболе. В частности, по этим кривым происходит движение всех комет Солнечной системы.

В наше время, когда вокруг Земли вращаются по эллиптическим орбитам тысячи искусственных спутников, когда к Луне, Венере, Марсу отправлены десятки космических станций, кривые второго порядка используются еще интенсивнее, чем прежде.