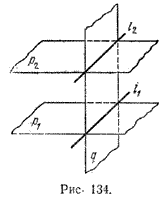
Глава IV. Прямые и плоскости в пространстве. Многогранники

§ 48. Параллельные плоскости

Две плоскости р и q называются параллельными, если они или совпадают или не имеют общих точек. Если р и q параллельны, то пишут р || q. Таким образом, р || q, если или
р = q или    p    q  =  .

Теорема 1. Если две параллельные плоскости пересечены третьей плоскостью, то прямые пересечения параллельны.

 Пусть параллельные плоскости p₁ и р₂ пересечены плоскостью q, и пусть
l ₁=  p₁    q,    l ₂=  p₂    q      (рис. 134).

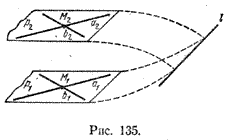
Рассмотрим существенный случай, когда p₁ и p₂ различные. В этом случае прямые l ₁ и l ₂ не могут иметь общих точек, так как их общая точка была бы общей для плоскостей p₁ и p₂ .

Таким образом, прямые l ₁ и l ₂  лежат в одной плоскости q и не имеют общих точек. Согласно определению l ₁ || l ₂ 

Докажем теперь следующий признак параллельности двух плоскостей.

Теорема 2. Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то эти плоскости параллельны.

Если плоскости p₁ и p₂ совпадают, то, согласно определению, p₁ || p₂.

Рассмотрим случай, когда p₁ и p₂ — различные плоскости. Пусть пересекающиеся прямые a₁ и b₁ плоскости  p₁  соответственно параллельны пересекающимся прямым a₂ и b₂ плоскости p₂: a₁ || a₂ и b₁ || b₂ (рис. 135).

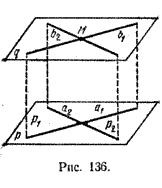
Методом «от противного» докажем, что плоскости p₁ и p₂ не пересекаются.

Предположим, что  p₁ и p₂ пересекаются и p₁    p₂ = l .
Из признака параллельности прямой и плоскости следует, что a₁ || p₂, b₁ || p₂, и поэтому
(см. теорему 1 § 47) a₁  || l и b₁ || l, что невозможно, так как a₁ и b₁ пересекаются.

Задача. Построить плоскость, проходящую через заданную точку М параллельно данной плоскости р.

В плоскости р возьмем две пересекающиеся прямые a₁ и a₂ (рис. 136).

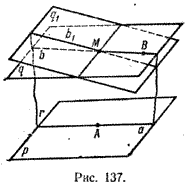
Затем через точку М и прямую  a₁ проводим плоскость p₁ , а через точку М и прямую a₂ — плоскость p₂.
В плоскости p₁ через точку  М  проведем прямую b₁ параллельно прямой a₁. Аналогично, в плоскости p₂ через М проведем прямую b₂ || a₂.
Плоскость q, проходящая через пересекающиеся прямые b₁  и b₂, будет искомой.

Теорема 3. Через точку, не лежащую в данной плоскости, можно провести единственную плоскость, параллельную данной.

Уже доказано, что через точку М, не лежащую в плоскости р, можно провести плоскость q || р.

Докажем методом от противного, что эта плоскость единственная.
Предположим, что через точку М проходят две различные плоскости q и q₁ параллельные плоскости р (рис. 137).

В плоскости q выберем некоторую точку В, не принадлежащую плоскости q₁. Через точки М, В и некоторую точку А  р проведем плоскость r.
Из теоремы 1 следует, что прямая а = р  r параллельна прямой b = q  r и прямой
b₁ = q₁  r, что невозможно, так как прямые b и b₁ пересекаются в точке М.