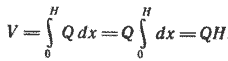Глава VII. Объемы тел и площади поверхностей.

§ 87*. Объем  произвольного цилиндра

Теорема 1. Объем произвольного цилиндра равен произведению площади его основания на высоту, т. е.

V = QH,        (1)

где Q — площадь основания, а Н — высота цилиндра.

Выберем за направление оси Ох направление, перпендикулярное плоскости основания данного цилиндра (рис. 263).

Тогда цилиндр можно рассматривать как тело с параллельными сечениями, площадь которых равна Q. Поэтому, используя формулу (1) из § 83, получаем

Следствие 1. Объем призмы равен произведению площади ее основания на высоту.

Действительно, призма—это цилиндр, основанием которого является многоугольник.  

Следствие 2. Если основанием цилиндра является эллипс с полуосями а и b, то

V = πаbН,      (2)

где Н — высота цилиндра.

В частности, если основанием цилиндра является круг радиуса R, то

V= πR²H.       (3)

Площадь основания (рис. 264) вычисляется по формуле

Для вычисления интеграла сделаем замену

x = a cos t,     t   [0; π];
dx = — a sin t dt

Тогда

Следовательно, площадь фигуры, ограниченной эллипсом с полуосями а и b,
равна πab.

Подставив найденное значение для Q в формулу (1), получим формулу (2). В частности, если а = b = R, то получим формулу (3).

Теорема 2. Объем наклонного цилиндра равен произведению площади его перпендикулярного сечения на длину образующей.

Докажем эту теорему лишь в частном случае, когда цилиндр является призмой. Для призмы теорема 2 формулируется следующим образом:

объем наклонной призмы равен произведению площади ее перпендикулярного сечения на длину бокового ребра.

Так как любую призму можно разбить на треугольные призмы, сумма объемов которых равна объему данной призмы, то доказательство достаточно провести для треугольной призмы.

Рассмотрим наклонную призму ABCA₁B₁C₁ (рис.265).

Пусть l — длина бокового ребра, Q — площадь основания, а Н — высота призмы. Через α обозначим величину  угла между плоскостью основания и плоскостью перпендикулярного сечения призмы.

Так как высота призмы OA₁ образует с боковым ребром AA₁ угол величины α , то из  /\ AA₁O получаем: Н = l cos α. Поэтому

V =QH = Q l cos α = ql,

где q = Q cos α  — площадь перпендикулярного сечения призмы.

Задача. Длина бокового ребра треугольной призмы равна 15 см, а расстояния между боковыми ребрами равны 17 см, 25 см, 26 см. Найти объем призмы.

Перпендикулярное сечение данной призмы — это треугольник со сторонами длины 17 см, 25 см и 26 см. Как нетрудно подсчитать, его площадь равна 204 см². Поэтому в силу теоремы 2

V = 204 см² •15 см = 3060 см³.