ВЫЧИСЛЕНИЕ ДЛИНЫ ОКРУЖНОСТИ И ЕЁ ЧАСТЕЙ.

12.  (226.) Предварительное разъяснение. Отрезок прямой можно сравнить с другим отрезком прямой, принятым за единицу, так как прямые линии при наложении совмещаются. Действительно, только по этой причине мы можем установить, какие отрезки прямых считать равными и неравными; что такое сумма отрезков прямой; какой отрезок больше другого в 2, 3, 4, ... раза и т. п. Точно так же дуги окружностей одинакового радиуса можно сравнить между собой вследствие того, что такие дуги при наложении  совмещаются. Но так как  никакая часть окружности (или другой кривой) не может совместиться с прямой, то нельзя путём наложения установить, какой криволинейный отрезок должно считать равным данному прямолинейному отрезку, а следовательно, и то, какой криволинейный отрезок больше данного прямолинейного в 2, 3, 4, ... раза. Таким образом, является необходимость особо определить, что мы будем   подразумевать   под   длиной   окружности   (или части её), когда сравниваем её с прямолинейным отрезком.

Для этой цели мы должны ввести новое понятие, имеющее исключительно большое значение во всей математике, именно понятие о пределе.

Предел числовой последовательности.

13.   (227.) Во многих вопросах алгебры и геометрии приходится встречаться с последовательностями чисел,  написанных одно за другим  по  определённому  закону.  Например,  натуральный ряд чисел:

1, 2, 3, 4, 5, ....

арифметическая и геометрическая прогрессии, продолженные неограниченно:

а, а + d, a + 2d, a + 3d, ...,
а, аd, аd², аd³, ...,

представляют собой бесконечные последовательности чисел,  или бесконечные числовые последовательности.

Для каждой такой последовательности можно указать правило, по которому составляются её члены. Так, в арифметической прогрессии каждый член разнится от предыдущего на одно и то же число, в геометрической прогрессии каждый член равен предшествующему, умноженному на некоторое определённое число (знаменатель прогрессии).

Многие последовательности составляются по более сложным правилам. Так, например, вычисляя √2  с недостатком сначала с точностью до 0,1, затем с точностью до 0,01, затем с точностью до 0,001 и продолжая это вычисление неограниченно, мы получим бесконечную числовую последовательность:

1,4; 1,41; 1,414; 1,4142.....,

дающую приближённое значение √2  с возрастающей степенью точности.

Для этой последовательности нельзя указать простого правила, по которому можно было бы получить новые её члены, зная предыдущие, но всё же можно определить любой член этой последовательности. Так, чтобы получить 4-й её член, нужно вычислить √2  с точностью до 0,0001, для получения 5-го члена нужно вычислить √2  с точностью до 0,00001 и т. д.

Допустим, что члены данной бесконечной последовательности a₁,a₂, a₃,...a_n,... по мере повышения их номера неограниченно приближаются к некоторому числу А. Это значит следующее: существует некоторое число А такое, что, какое бы малое положительное число q мы ни взяли, в данной последовательности можно отыскать член, начиная с которого все члены последовательности по абсолютной величине отличаются от А меньше, чем на q. Мы будем это свойство коротко выражать так: абсолютная величина разности а_п — А неограниченно убывает с возрастанием номера п.

В этом случае число А называется пределом данной бесконечной числовой последовательности. Приведём пример такой последовательности.  Составим последовательность десятичных дробей:

0,9;   0,99;   0,999; ... .

Здесь каждый член получается из предыдущего приписыванием нового десятичного знака 9.

Легко заметить, что члены этой последовательности неограниченно приближаются к единице.

Именно, первый член отличается от единицы на 0,1, второй на 0,01, третий на 0,001, и если достаточно продолжить эту последовательность, то можно найти в ней член, начиная с которого все последующие члены будут отличаться от единицы на сколь угодно малую, заранее указанную величину. Следовательно, мы можем cказать, что взятая нами бесконечная числовая последовательность имеет пределом единицу. Другим примером числовой последовательности, имеющей предел, служит последовательность приближённых значений длины отрезка, несоизмеримого с единицей длины, вычисленных с недостатком, сначала с точностью до 0,1, затем — до 0,01, затем — до 0,001 и т. д.

Пределом этой последовательности служит бесконечная десятичная дробь, представляющая точную меру длины данного отрезка. В самом деле, величина бесконечной десятичной дроби заключена между двумя её приближёнными значениями, вычисленными с одинаковой  точностью — одно  с  недостатком,   другое  с  избытком.

Как было показано выше, эта разность неограниченно убывает по мере повышения степени точности приближённых значений. Следовательно, должна неограниченно убывать и разность между самой бесконечной десятичной дробью и её приближёнными значениями по мере повышения степени точности этих значений. Значит, бесконечная десятичная дробь служит пределом последовательности всех её приближённых значений, взятых с недостатком (или всех приближённых значений, взятых с избытком).

Легко заметить, что не всякая бесконечная последовательность имеет предел; например, натуральный ряд чисел:

1, 2, 3, 4, 5.....

очевидно, никакого предела не имеет, так как его члены неограниченно возрастают и ни к какому числу не приближаются.

14.    (228.)   Теорема.   Всякая   бесконечная   числовая последовательность может иметь только один предел.

В справедливости этой теоремы легко убедиться доказательством от противного. В самом деле, предположим, что дана последовательность

a₁,a₂, a₃,...a_n,...,

которая имеет два различных предела А и В. В таком случае, в силу того, что А есть предел данной последовательности, абсолютная величина разности a_n — А должна неограниченно убывать с возрастанием п. В силу того, что В есть тоже предел данной последовательности, абсолютная величина разности a_n — В также должна неограниченно убывать с возрастанием п.

Но в таком случае абсолютная величина разности

(a_n — А) — (a_n — В)

должна также или неограниченно убывать, или быть равной нулю. Но эта последняя разность равна разности чисел В — A и, следовательно, есть некоторое вполне определённое, отличное от нуля число. Это число не зависит от номера п и при возрастании  п вовсе не изменяется. Таким образом, предположение, что существуют два предела числовой последовательности, привело нас к противоречию.

15.  (229.) Предел  возрастающей  бесконечной  числовой  последовательности.   Рассмотрим такую  последовательность  a₁,a₂, a₃,...a_n,...,  в   которой   каждый    следующий    член    больше предыдущего, т. е. a_n+1 > a_n, и в то же время все члены последовательности меньше некоторого определённого числа М, т. е. для любого номера п
 a_n < М.

В этом случае последовательность имеет определённый предел. (Теорема Вейерштрасса).

16.  (231.) Предел переменной величины.   Если дана последовательность

a₁,a₂, a₃,...a_n,...,

то п-й член её a_n можно назвать переменной величиной, числовое значение которой зависит от её номера п. Этим выражением «переменная величина» часто пользуются для упрощения речи. Так, вместо выражения "дана бесконечная числовая последовательность a₁,a₂, a₃,...a_n,..." принято говорить "дана переменная величина a_n, принимающая последовательно ряд значений a₁,a₂, a₃,...". Если пользоваться этим способом выражения, то можно говорить не о пределе последовательности,  а о пределе переменной величины.

В таком случае, предложение, доказанное в § 14 (228), можно высказать в форме: «Всякая переменная величина может стремиться лишь к одному пределу». Это предложение часто высказывают так: «Если даны две переменные величины a_n и b_n, причём все значения первой равны соответствующим значениям второй: a₁ = b₁, a₂ = b₂, ..., a_n = b_n, то предел первой величины, конечно, если он существует, равен пределу второй», или короче: «Если две переменные величины равны, то равны и их пределы».

Предложение (§ 15) о пределе возрастающей числовой последовательности можно высказать так: если переменная величина а_n возрастает с возрастанием номера п и в то же время остаётся меньше некоторого постоянного числа, то эта переменная  величина имеет предел.

Длина окружности.

17.   (232.) Понятие о пределе даст возможность точно определить, что мы подразумеваем под длиной окружности.  Предварительно   докажем   следующие   леммы.

Лемма 1. Выпуклая ломаная (ABCD, черт. 18) меньше всякой другой ломаной (AEFGD), объемлющей первую.

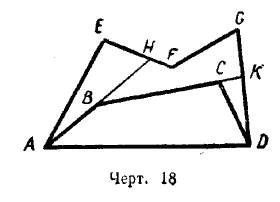
Выражения «объемлющая ломаная», «объемлемая ломаная» имеют следующий смысл. Пусть две ломаные (как те, которые изображены у нас на чертеже) имеют одни и те же концы А и D и расположены таким образом, что одна ломаная (ABCD) вся лежит внутри многоугольника, образованного другой ломаной и отрезком AD, соединяющим концы А и D; тогда внешняя ломаная называется объемлющей, а внутренняя ломаная — объемлемой.

Предстоит доказать, что объемлемая ломаная ABCD (если она выпуклая) короче всякой объемлющей линии AEFGD (все равно — выпуклой или невыпуклой), т. е. что

АВ + ВС + CD < АЕ + EF + FG + GD.

Продолжим стороны выпуклой ломаной так, как указано на чертеже. Тогда, приняв во внимание, что отрезок прямой меньше всякой ломаной, соединяющей концы отрезка, мы можем написать следующие неравенства:

АВ + ВН < АЕ + ЕН;

ВС + СК< ВН + HF + FG + GK;

CD < CK + KD.

Сложим почленно все эти неравенства и затем от обеих частей полученного неравенства отнимем вспомогательные отрезки ВH и СК, далее, заменив сумму EH + HF отрезком EF и сумму GK + KD — отрезком GD, получим то неравенство, которое требовалось доказать.

Замечание. Если бы объемлемая линия не была выпуклой (черт. 19), то изложенное доказательство нельзя было бы применить. В этом случае объемлемая ломаная может оказаться и больше объемлющей.

18. (233.) Лемма 2. Периметр выпуклого многоугольника (ABCD) меньше периметра всякого другого многоугольника (MNPQRL), объемлющего первый (черт. 20).

Требуется доказать, что

АВ + ВС + CD + DA < LM + MN + NP + PQ + QR + RL.

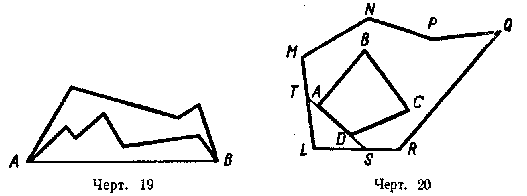
Продолжив в обоих направлениях одну какую-нибудь сторону AD выпуклого многоугольника, применим к ломаным линиям ABCD и ATMNPQRSD, соединяющим точки А и D, лемму предыдущего параграфа; получим неравенство:

АВ + ВС + CD < AT + TM + MN + NP + PQ+ QR + RS + SD.

С другой стороны, так как отрезок ST меньше ломаной SLT, то можем написать:

ТА + AD + DS < TL + LS.

Сложим почленно эти два неравенства и отнимем от обеих частей вспомогательные отрезки AT и DS; далее, заменив сумму TL + ТМ отрезком LM и сумму LS + RS отрезком LR, получим то, что требовалось доказать.

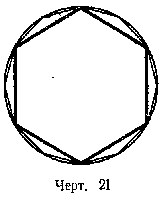
19. (234.) Определение длины окружности. Впишем в данную окружность (черт. 21) правильный многоугольник, например шестиугольник, и на какой-нибудь прямой MN (черт. 22) отложим отрезок ОP₁ равный периметру этого шестиугольника (на нашем чертеже периметр изображён по недостатку свободного места в уменьшенном виде).

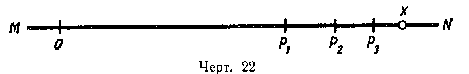
Удвоим теперь число сторон вписанного шестиугольника, т. е. вместо шестиугольника возьмём правильный вписанный 12-угольник. Найдём также его периметр и отложим его на той же прямой MN от той же точки О; пусть тогда получится отрезок ОP₂, который должен быть больше ОP₁ так как вместо каждой стороны шестиугольника мы теперь берём ломаную (из двух сторон 12-угольника), которая длиннее прямой. Удвоим снова число сторон вписанного 12-угольника, т. е. возьмём теперь правильный 24-угольник (на чертеже он не указан), найдём его периметр и отложим его на MN от той же точки O; мы получим тогда отрезок ОP₃, который будет больше ОP₂ по той же причине, по какой ОP₂ больше ОP₁.

Вообразим, что такой процесс удвоения и откладывания периметров продолжается всё далее и далее. Тогда мы получим бесконечную последовательность периметров
ОP₁, ОP₂, ОP₃, ... которая является возрастающей последовательностью. Однако возрастание это не может быть неограниченным, так как периметр всякого вписанного многоугольника (выпуклого), каково бы ни было число его сторон, всегда остаётся меньше периметра любого описанного многоугольника (как его объемлющего). Вследствие этого полученная последовательность периметров правильных вписанных многоугольников имеет определённый предел (§ 15). Этот предел и принимают за длину окружности. Таким образом, мы принимаем следующее определение: за длину окружности принимается тот предел, к которому стремится (приближается) переменный периметр правильного многоугольника, вписанного в эту окружность, когда число сторон его неограниченно удваивается.

Замечание.    Можно доказать (мы опускаем это доказательство), что предел   этот   не   зависит   от   того,  с   какого   многоугольника   мы   начинаем удвоение. Более того, можно доказать, что если даже вписанные многоугольники и не будут правильные, все же периметры их стремятся к тому же самому пределу, как и периметры правильных многоугольников, лишь бы только стороны их неограниченно уменьшались (и, следовательно, число сторон их неограниченно увеличивалось) путём ли удвоения, как мы это предполагали для правильных многоугольников, или по какому-нибудь иному закону (мы опускаем это доказательство).

Таким образом, для каждой окружности существует свой единственный предел, к которому стремится периметр вписанного выпуклого многоугольника, когда стороны его неограниченно уменьшаются; предел этот и принимается за длину окружности.

Равным образом за длину какой-нибудь дуги окружности АВ (черт. 23) принимается предел, к которому стремится переменный периметр ломаной линии, вписанной в эту дугу и имеющей с ней одни и те же концы, когда число сторон ломаной неограниченно удваивается.

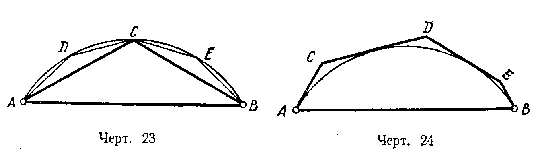
20.  (235.) Допущения.  Для  простоты  изложения  мы   примем без доказательства  следующие,   почти  очевидные,   предложения:

Длина дуги окружности: 1) больше стягивающей её хорды, но 2) меньше периметра всякой ломаной линии, описанной около этой дуги и имеющей с ней одни и те же концы (черт. 24).

21.   Нахождение длины окружности. Для этой цели можно воспользоваться формулой,  выражающей  сторону  (a_n) правильного n - угольника через радиус (R) описанного круга:

a_n = 2R • sin ^180°/_n .

Тогда периметр n-угольника (Р_n) можно выразить в виде формулы:

P_n = a_nn = 2Rn • sin ^180°/_n .

Пользуясь    семизначными    таблицами    синусов    углов,   найдём

 Р₆   = 2R• 6 sin 30° = 2R • 3.
 P_l2  = 2R • 12 sin 15° = 2R • 3,10582...
 Р₂₄  = 2R •  24 sin 7°30' = 2R • 3,13262...
 P₄₈  = 2R • 48 sin 3°45' = 2R • 3,13935...
 Р₉₆  = 2R  •  96 sin 1°52'30" = 2R • 3,14103...
 Р₁₉₂ = 2R • 192 sin 56'15" = 2R • 3,14145...
 Р₃₈₄ = 2R • 384 sin 28'7",5 = 2R • 3,14156....
 

При каждом последующем удвоении числа сторон правильного вписанного многоугольника мы получаем последовательность значений произведения 2Rn • sin ^180°/_n.   Каждый    последующий   член этой последовательности больше предыдущего и в то же время каждый её член меньше некоторого определённого числа. Эта последовательность, как показано в § 19 (234), имеет предел, который и принимают за длину окружности. Таким образом, периметр правильного вписанного многоугольника даёт приближённое значение длины окружности, причём по мере продолжения процесса удвоения числа сторон этого многоугольника точность значения возрастает.

22. (238.) Отношение длины окружности к диаметру. Рассматривая процесс нахождения длины окружности, можно заметить, что число, на которое нужно умножить диаметр, чтобы получить длину окружности, не зависит от величины самого диаметра, так что если мы нашли, что длина какой-нибудь окружности равна её диаметру, умноженному на некоторое число, то и длина всякой другой окружности будет равна её диаметру, умноженному на то же самое число.

В самом деле, возьмём две окружности: одну радиуса R, другую радиуса r. Длину первой окружности обозначим через С, длину второй — через с. Впишем в каждую из них правильный многоугольник с одним и тем же числом сторон и будем удваивать число сторон каждого из этих многоугольников.

Обозначим через Р_п переменный периметр правильного многоугольника, вписанного в первую окружность, и через р_п переменный периметр правильного многоугольника с тем же числом сторон, вписанного во вторую окружность.

На основании   формулы  P_n = 2Rn • sin ^180°/_n , данной в § 21, мы можем    написать:  
.

Переменный периметр Р_n имеет пределом длину С первой окружности. Переменный периметр р_n имеет пределом длину с второй окружности. А   потому из равенства      вытекает   ^C/_2R = ^c/_2r     (§ 14 и 16).
Таким образом, мы можем сказать, что отношение длины окружности к её диаметру есть число постоянное для всех окружностей.

Это постоянное число принято обозначать греческой буквой π . Обозначение это введено, по всей вероятности, в XVII столетии. Буква π  (пи) есть начальная буква греческого слова περιφερεια (окружность).

Мы можем, таким образом, для длины С окружности написать такую формулу:

С = 2R • π,    или    С = 2πR.

Доказано, что число π является числом иррациональным, и, значит, оно не может быть выражено точно никаким рациональным числом. Но его приближённые значения можно находить различными способами с какой угодно точностью. Приняв периметр вписанного 96-угольника за приближённую длину окружности, мы получим для π приближённое значение 3,14 с недостатком и с точностью до 0, 01. Эта точность для практических целей часто бывает достаточна. Для более точных вычислений можно брать
π ≈ 3,14159.

Пользуясь современными вычислительными машинами, нашли более 3000 знаков числа π.

Полезно заметить, что еще в III веке до начала нашей эры знаменитый сиракузский геометр Архимед нашёл для π очень простое число²²/₇ т. е. 3 ¹/₇. Это число несколько более π и разнится от него менее чем на 2 тысячных.

При решении геометрических задач часто встречается число, обратное числу π, т. е. равное дроби  ¹/_π. Полезно запомнить  несколько цифр этого числа:

¹/_π = 0,3183098 ...

23.  (239.) Длина дуги, содержащей п градусов. Длина окружности есть 2πR, значит, длина дуги в 1° равна  ^2πR/₃₆₀ = ^πR/₁₈₀;    следовательно, длина s дуги, содержащей п°, выразится так:

s = ^πRn/₁₈₀

Если дуга выражена в минутах (') или в секундах ("), то длина её определяется соответственно формулами:

s = ^πRn/_180•60   или    s = ^πRn/_{180•60 •60} ,

где п — число минут или секунд.

24.   (240.) Задача. Вычислить с точностью до 1 мм радиус такой окружности, дуга которой,   содержащая 81°21'36", равна 0,452 м.

Обратив 81°21'36" в секунды, получим число 292 896. Из уравнения

0, 452 = ^πR•292896/_{180•60 •60}

находим:

R = ^{0,452•180•60•60}/_292896π = ¹/_π = 0,318 (м)

25.   (241.)    Задача.    Определить число градусов дуги, длина которой равна радиусу.

Заменив в формуле, определяющей длину дуги в п°, величину s на R, получим уравнение:

R = ^πRn/₁₈₀,   или  1 = ^πn/₁₈₀,

откуда

п° = ^180°/_π = 180° • ¹/_π = 180° • 0,3183098 = 57°295764 = 57°17'44",8.

Заметим, что дуга, равная радиусу, называется радианом.