ПЛОЩАДЬ   КРУГА   И   ЕГО   ЧАСТЕЙ.

26.  (262.) Лемма. При неограниченном удвоении числа сторон правильного вписанного многоугольника сторона его может сделаться как угодно малой.

Пусть п есть число сторон правильного вписанного многоугольника и р — его периметр; тогда длина одной стороны этого многоугольника выразится дробью ^p/_n. При  неограниченном удвоении числа сторон многоугольника знаменатель этой дроби будет, очевидно, возрастать неограниченно, а числитель, т. е. р, хотя и будет возрастать, но не беспредельно (так как периметр всякого вписанного выпуклого многоугольника всегда остаётся меньшим периметра любого описанного многоугольника). Если же в какой-нибудь дроби знаменатель неограниченно возрастает, а числитель остаётся меньше некоторой постоянной величины, то дробь эта может сделаться как угодно малой. Значит, то же самое можно сказать о стороне правильного вписанного многоугольника: при неограниченном удвоении числа сторон она может сделаться как угодно малой.

27.   (263.) Следствие.   Пусть АВ (черт. 25) есть сторона правильного вписанного многоугольника, ОА — радиус и ОС — апофема. Из  /\ ОАС находим:

АО — ОС< АС,    т. е.

АО — ОС<  ¹/₂AB.

Но при неограниченном удвоении числа сторон правильного вписанного многоугольника сторона его, как мы сейчас доказали, может сделаться как угодно малой, значит, то же самое можно сказать и о разности АО — ОС. Таким образом, при неограниченном удвоении числа сторон правильного вписанного многоугольника разность между радиусом и апофемой может сделаться как угодно малой. Это же можно высказать другими словами так: при неограниченном удвоении числа сторон правильного вписанного многоугольника предел, к которому стремится апофема, есть радиус.

28.  (264.) Площадь круга. Впишем в круг, радиус которого обозначим R, какой-нибудь правильный многоугольник. Пусть

 площадь этого многоугольника будет q,
 периметр       »           »             »           р,
 апофема         »           »             »           а.

По формуле вычисления площади правильного многоугольника имеем:

q =  ¹/₂ pa.

Вообразим теперь, что число сторон этого многоугольника неограниченно удваивается. Тогда периметр р и апофема а (следовательно, и площадь q) будут увеличиваться, причём периметр будет стремиться к пределу, принимаемому за длину С окружности, апофема будет стремиться к пределу, равному радиусу R круга. Из этого следует, что площадь многоугольника, увеличиваясь при удвоении числа сторон, будет стремиться к пределу, равному  ¹/₂ С • R. Предел этот принимается за численную величину площади круга. Таким образом, обозначив площадь круга буквой К, можем написать:

K = ¹/₂ С • R,

т. е. площадь круга равна половине произведения длины окружности на радиус.

Так как С = 2πR, то

К = ¹/₂ • 2πR • R = πR²,

т. е. площадь круга равна квадрату радиуса, умноженному на отношение длины окружности к диаметру.

29.   (265.)  Следствие.   Площади  кругов   относятся, как квадраты радиусов или диаметров.

Действительно, если K и K₁ будут площади двух кругов, a R и R₁ — их радиусы, то

K =  πR²    и    K₁ =  πR₁² ,

откуда

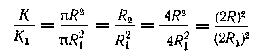
30.   (266.)   Зада.ча   1.   Вычислить  площадь   круга,    длина окружности которого равна 2 м.

Для этого предварительно находим радиус R из равенства:

2πR = 2, откуда   R = ¹/_π  = 0,3183...   .

Затем определим площадь круга:

K = πR² = π(  ¹/_π )²=  ¹/_π = 0,3183 ... м² .

31.   (267.) Задача  2.     Построить  квадрат,  равновеликий данному кругу.

Эта задача, известная под названием квадратуры к р у г а, не может быть решена при помощи циркуля и линейки. Действительно, если обозначим буквой х сторону искомого квадрата, а буквой R радиус круга, то получим уравнение:

х²  = πR² ,

откуда

πR : х = х : R,

т. е. х есть средняя пропорциональная между полуокружностью и радиусом. Следовательно, если известен отрезок, длина которого равна длине полуокружности, то легко построить квадрат, равновеликий данному кругу, и, обратно, если известна сторона квадрата, равновеликого кругу, то можно построить отрезок, равный по длине полуокружности. Но с помощью циркуля и линейки нельзя построить отрезок, длина которого равнялась бы длине полуокружности; следовательно, нельзя в точности решить задачу о построении квадрата, равновеликого кругу. Приближённое решение можно выполнить, если предварительно найти приближённую длину полуокружности и затем построить среднюю пропорциональную между отрезком этой длины и радиусом.

32.  (268.) Теорема. Площадь сектора равна произведению длины его дуги на половину радиуса.

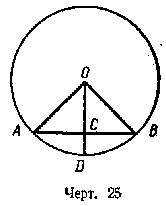
Пусть дуга АВ (черт. 26) сектора АОВ содержит п°. Очевидно, что площадь сектора, дуга  которого  содержит   1°,   составляет   ¹/₃₆₀  часть площади круга, т. е. она равна
. Следовательно, площадь S сектора, дуга которого содержит п°, равна:

Так как дробь — выражает длину дуги АВ (§ 23), то, обозначив её буквой s, получим:

S= s • ^R/₂

33. (269.) Площадь сегмента. Для нахождения площади сегмента, ограниченного дугой s и хордой АВ, надо отдельно вычислить площадь сектора AOBsA и площадь треугольника АОВ. Затем из площади сектора AOBsA вычесть площадь треугольника АОВ, если дуга сегмента меньше 180°. Если же дуга сегмента больше 180°, то к площади сектора AOBsA надо прибавить площадь треугольника АОВ (черт. 26 и 27).