ГЛАВА ПЕРВАЯ ПРЯМЫЕ И ПЛОСКОСТИ
Задачи на построение
36. Через данную точку (С) в пространстве провести плоскость, перпендикулярную к данной прямой (АВ, черт. 22).
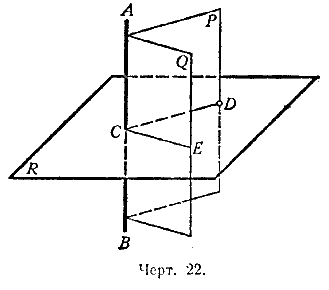
Решение. 1-й случай. Данная точка С лежит на прямой АВ (черт. 22).
Проведём через прямую АВ какие-нибудь две плоскости Р и Q. Искомая плоскость должна пересекать эти плоскости по прямым, перпендикулярным к прямой АВ (§ 24). Отсюда построение:
через АВ проводим две произвольные плоскости Р и Q.
В каждой из этих плоскостей восставляем перпендикуляр к прямой АВ в точке С (в плоскости Р —перпендикуляр СD, в плоскости Q—перпендикуляр СЕ).
Плоскость, проходящая через прямые CD и СЕ, есть искомая.
2-й случай. Данная точка не лежит на прямой АВ (черт. 22).
Через точку D и прямую АВ проводим плоскость Р и в этой плоскости строим прямую DC, перпендикулярную к АВ.
Через прямую АВ проводим произвольно вторую плоскость Q и в этой плоскости строим прямую СЕ, перпендикулярную к АВ.
Искомая плоскость должна пересечь плоскости Р и Q по прямым, перпендикулярным к АВ. Отсюда построение:
через точку D проводим в плоскости P прямую DС, перпендикулярную к АВ.
Прямая DС пересечёт прямую АВ в некоторой точке С.
Через точку С проводим в плоскости Q прямую СЕ перпендикулярную к АВ.
Плоскость, проходящая через прямые СD и СE — искомая.
Так как в каждой из плоскостей Р и Q через данную точку провести лишь, одну прямую, перпендикулярную к данной, то задача в обоих случаях имеет одно решение, т. е. через каждую точку в пространстве можно провести лишь одну плоскость , перпендикулярную к данной прямой.
36. Через данную точку (О) пространства провести прямую, перпендикулярную к данной плоскости (Р).
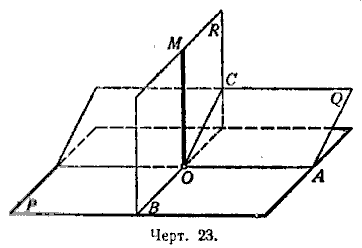
1-й случай. Точка О лежит на плоскости Р (черт. 23). Проведём на плоскости Р через точку О две какие-либо взаимно перпендикулярные прямые ОА и ОВ. Проведём, далее, через прямую ОА какую-либо новую плоскость Q и на этой плоскости Q построим прямую ОС, перпендикулярную к ОА. Через прямые ОВ и ОС проведём новую плоскость R и построим в ней прямую ОМ, перпендикулярную к ОВ. Прямая ОМ и будет искомым перпендикуляром к плоскости Р.
Действительно, так как ОА _|_ ОВ и ОА _|_ ОС, то прямая АО перпендикулярна к плоскости R и, следовательно, ОА _|_ ОМ.
Таким образом, мы видим, что ОМ _|_ ОА и ОМ _|_ ОВ; следовательно, ОМ перпендикулярна к плоскости Р.
2-й случай. Точка О не лежит на плоскости Р (черт. 24).
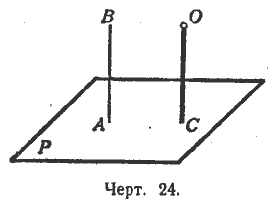
Возьмём на плоскости Р какую-нибудь точку А и выполним для неё предыдущее построение. Мы получим тогда прямую АВ, перпендикулярную к плоскости Р. После этого через точку О проводим прямую, параллельную АВ. Эта прямая и будет искомой (§ 31).
Задача в обоих случаях имеет одно решение. В самом деле, так как два перпендикуляра к одной и той же плоскости параллельны, то через одну и ту же точку О нельзя провести двух перпендикуляров к плоскости Р. Следовательно, через каждую точку в пространстве можно провести одну и только одну прямую, перпендикулярную к данной плоскости.
37. Пример более сложной задачи. Даны две скрещивающиеся прямые (а и b, черт. 25). Построить прямую, пересекающую обе данные прямые и перпендикулярную к ним обеим.
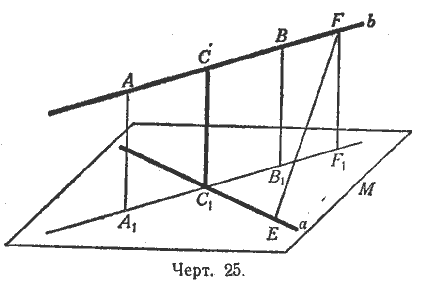
Решение. Проведём через прямую а плоскость М, параллельную прямой b (§ 21). Из двух каких-нибудь точек прямой b опустим перпендикуляры АА1 и ВВ1 на плоскость М. Соединим точки А1 и В1 отрезком прямой и найдём точку С1 пересечения прямых
А1В1 и а. Через точку С1 проведём прямую, перпендикулярную к плоскости М. Предоставляем самим учащимся доказать, что эта прямая: 1) пересечётся с прямой b в некоторой точке С и 2) будет перпендикулярна как к прямой а, так и к прямой b.
Прямая СС1 будет, следовательно, искомой прямой.
Заметим, что отрезок СС1 меньше всех других отрезков, которые можно получить, соединяя точки прямой а с точками прямой b. В самом деле, возьмём на прямой а какую-нибудь точку E и на прямой b какую-нибудь точку F , соединим эти точки отрезком прямой и докажем, что ЕF > СС1.
Опустим из точки F перпендикуляр FF1 на плоскость M, Тогда будем иметь:
ЕF > FF1 (§ 26). Но FF1 = CC1, следовательно, EF >СС1. На этом основании длина отрезка CC1 называется кратчайшим расстоянием между данными прямыми а и b.