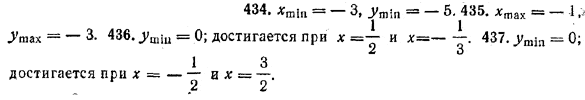КВАДРАТНЫЙ ТРЕХЧЛЕН  III

§ 60. Экстремальное значение функции у = ах²+ bх +с

Наименьшее, или минимальное, из всех значений, которые принимает квадратная функция у = ах²+ bх +с, геометрически можно истолковать как ординату самой низкой точки параболы у = ах²+ bх +с (рис. 81), а наибольшее, или максимальное, значение — как ординату самой высокой точки параболы у = ах²+ bх +с (рис.   82).

Если а > 0, то парабола у = ах²+ bх +с уходит неограниченно вверх (рис. 81). В этом случае самой высокой точки параболы не существует. Поэтому не существует и максимального значения функции у = ах²+ bх +с. Но в этом случае существует самая низкая точка параболы — ее вершина. Следовательно, существует минимальное значение функции. Это минимальное значение (мы будем его обозначать y_min) равно ординате вершины параболы. Абсцисса этой вершины (обозначим ее  х_min дает то значение аргумента х, при котором достигается минимум функции у = ах²+ bх +с.

Если а < 0, то парабола у = ах²+ bх +с  уходит неограниченно вниз (рис. 82). В этом случае самой низкой точки параболы не существует. Поэтому не существует и минимального значения функции у = ах²+ bх +с. Зато существует самая высокая точка параболы — ее вершина. Следовательно, существует максимальное значение данной функции. Это максимальное значение (мы будем обозначать его y_mах) равно ординате вершины параболы. Абсцисса этой вершины (обозначим ее х_mах) дает то значение аргумента х, при котором достигается максимум функции у = ах²+ bх +с.

В § 57 было установлено, что вершина параболы у = ах²+ bх +с независимо от того, положительно а или отрицательно, имеет координаты:

                 (1)

Поэтому можно сказать, что если а > 0, то функция у = ах²+ bх +с принимает наименьшее значение ; наибольшего значения этой функции не существует.

Если а <. 0, то  функция  у = ах²+ bх +с   принимает   наибольшее    значение

наименьшего  значения функции в данном случае не существует.

Минимальные и максимальные значения функции иначе называются экстремальными.

Пример 1. Найти экстремальное значение функции у = 2х² —  4х — 17 и указать, при каком значении х функция принимает это экстремальное значение.

Поскольку коэффициент при х² положителен, то данная функция имеет минимальное значение. Максимального значения она не имеет. Чтобы определить минимальное значение, найдем координаты вершины параболы у =  2х² —  4х — 17. Для этого выделим полный  квадрат:

2х² —  4х — 17= 2 (х² —  2х — ¹⁷/₂ ) = 2[(х² —  2х + 1) —1—¹⁷/₂ ] = 2(х— 1 )² — 19.

Отсюда заключаем, что координаты вершины параболы таковы: х = 1,  у = —19. (Эти координаты, конечно, можно было бы получить и по формулам (1), если в них положить а = 2, b = —4, с = —17.)

Следовательно, минимальное значение функции у = 2х² —  4х — 17 равно —19. Оно достигается при х = 1.

Пример 2. Найти экстремальное значение функции  у = — х²  — 4х + 6 и выяснить, при каком значении аргумента х оно достигается.

Поскольку коэффициент при х² отрицателен, то данная функция имеет максимальное значение. Минимального значения она не имеет. Чтобы найти максимальное значение, выделим полный квадрат:

— х²  — 4х + 6 = — (х²  + 4х² — 6) =  — [(х² + 4х + 4) — 10] = — (х + 2)² + 10.

Отсюда заключаем, что максимальное значение данной функции равно  10. Оно достигается при х = — 2.

Упражнения

Найти экстремальные значения данных функций и указать, при каких значениях аргумента они достигаются (№ 434—437).

434.  у = 2х²  + 12х + 13.

435. у  = — 2х²  — 4х — 5.

438.  у  = |6х²  — х — 1 |.

437.  у  = |4х²  — 4х — 3|.

438. Доказать, что если сумма двух величин постоянна, то их произвединие максимально тогда и только тогда, когда эти величины принимают равные значения. (Это утверждение является естественным обобщением теоремы о постоянной сумме на случай любых, а не только положительных величин; . см.  гл.  I, § 17.)

ОТВЕТЫ