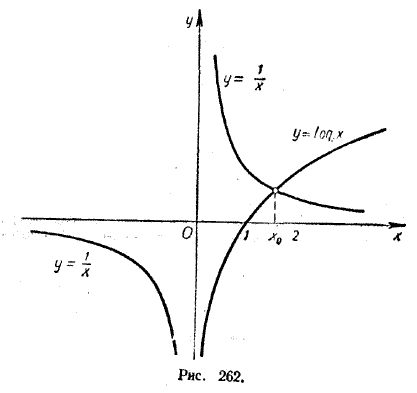ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ   VIII

§ 198. Примеры   графического  решения  показательных  и  
логарифмических уравнений

Пример   1.  Решить уравнение

2^х = 2х.

На одном и том же чертеже (рис. 260) построим графики двух функций: у = 2^х и у = 2х. Эти графики пересекаются в двух точках: А с абсциссой 1 и В с абсциссой 2. Поэтому данное уравнение имеет два корня: х = 1 и   х =2.

Пример 2.  Решить уравнение

lg х = х.

Графики функций y = lg х  и  y = x (рис. 261) не пересекаются друг с другом. Поэтому данное уравнение не имеет корней.

Мы рассмотрели простейшие примеры. Уравнения, которые получаются при решении практических задач, обычно значительно отличаются от таких «учебных» задач. Для их решения наряду с графической иллюстрацией приходится обращаться и к таблицам. Рассмотрим, например, такое уравнение.

log₂ x =  ¹/_x.

Графики функций у = log₂ x   и   у  =  ¹/_x (рис. 262) пересекаются в одной точке, абсцисса которой заключена между 1 и 2. Поэтому данное уравнение имеет один корень х₀, который больше 1, но меньше 2:

1 < х₀ < 2.

Возьмем точку х =1,5, являющуюся средной точкой интервала (1;2). В этой точке

log₂ x = log₂ ³/₂ = log₂3 — log₂2= ^lg3/_lg2 — 1.

Используя   таблицы В. М. Брадиса, находим, что

log₂ ³/₂ ≈ 0,58.

При   х =1,5   ¹/_x ≈ 0,66. Поскольку в точке х =1,5  log₂ x <  ¹/_x, искомый корень х₀  должен быть больше, чем 1,5 (см  рис   262) Теперь мы уверены, что

1,5 < х₀ < 2

«Испытаем» точку х =1,7 как одну из ближайших к средней точке интервала (1,5; 2,0). При х = 1,7 получаем, используя таблицы В. М. Брадиса,

log₂ x = ^lg1,7/_lg2 ≈ 0,76

 ¹/_x ≈ 0,58

Поскольку

log₂ 1,7 > ¹/_1,7 ,

искомый корень х₀  должен быть меньше, чем 1,7 (см. рис.  262). следовательно,

1,5 < х₀ < 1,7.

Поэтому с точностью до 0,1

х₀ ≈ 1,6.

Рассматривая точки интервала (1,5; 1,7), мы могли бы получить и более точное значение корня х₀. Попробуйте, например, самостоятельно получить приближенное значение х₀ с точностью до 0,01.

Упражнения

1470.   Решить графически уравнения:

а) 2^х = х + 2;        в) 2^х = x²;               д) log₂ x = ^x/₂;

б) 3^х = 3х;              г) log₂ x = x — 1;  е)  log₂ (х + 3) = 3 — х .

1471.   Найти корень уравнения   2^х = 2 — х    с точностью до 0,1.

1472.   Найти   наименьший   корень   уравнения   log₂ x = ¹/₃ х   с точностью до 0,1.

ОТВЕТЫ

1471  0,6.    1472.   1,40.