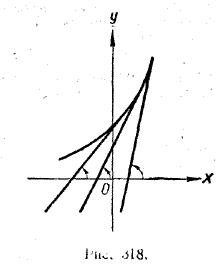ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 236. Применение производной   к   нахождению   участков   возрастания и
участков убывания функций

С помощью производной легко найти участки возрастания и участки убывания любой дифференцируемой функции. Имеет место следующая теорема.

Теорема. Если производная f '(x) функции  f (x) положительна в интервале [а, b], то функция f (x) монотонно возрастает в этом интервале. Если же производная отрицательна в этом интервале, то в нем функция f (x) монотонно убывает.

Доказательство этой теоремы выходит за пределы школьной программы. Поэтому мы ограничимся лишь ее геометрической  иллюстрацией.

Производная функции у = f (x)  при х = х₀ равна угловому коэффициенту касательной, проведенной к графику функции у = f (x) в точке с абсциссой х . Условие f '(x)  > 0 означает, что в рассматриваемом  интервале угловые коэффициенты касательных положительны. Но это возможно лишь в том случае, когда углы, образованные касательными с положительным направлением оси х, острые (рис. 318).

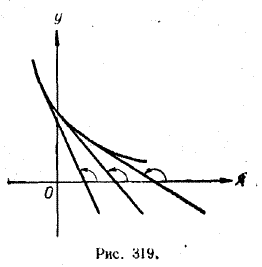
Тогда график функции у = f (x)  с ростом х поднимается все выше и выше A это и означает, что функция у = f (x)  монотонно  возрастает.

Случай, когда в интервале [а, b]   f '(x)  < 0 рассматривается аналогично.

Условие  f '(x)  < 0  означает, что угловые коэффициенты касательных к графику функции  у = f (x)  отрицательны. Но это возможно лишь в том случае, когда углы, образованные касательными с положительным направлением оси х, тупые (рис. 319).

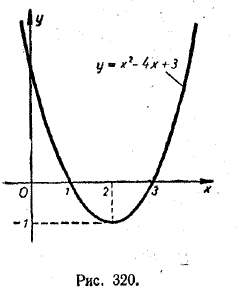
Тогда график функции у = f (x) с ростом х опускается все ниже и ниже. А это и означает, что функция у = f (x) монотонно убывает.

Пример. Определить участки возрастания  и  участки  убывания функции

f (x) = x²  — 4х + 3.

Имеем:

f '(x) = 2х — 4.

При х > 2    f '(x)  > 0, а при х < 2   f '(x)  < 0.

Значит,  функция  f (x) = x²  — 4х + 3  при х > 2 возрастает, а при х < 2 убывает ( рис. 320).

К такому же результату мы пришли бы, если бы исследовали данную функцию путем выделения полного квадрата (см. рис. 320):

 f (x) = x²  — 4х + 3 = x²  — 4х + 4 — 1 = (х — 2)² — 1.

Использование производной в данном случае легче и быстрее приводит к решению  задачи.

Упражнения

Определить участки возрастания    и участки убывания следующих функций:

1881.  у = 3 + 4х — х².                               1888. у  = 3х² + х.

1882.  у  = х³ — 3х + 1.                              1887. у  = √х³ — 3х.

1883.  у  = х⁴ — 2х³ — 3.                           1888. у  = х + ¹/_x.

1884.  у  = х³ + 6х² — 15х + 2.                   1889. у  = sin х — ¹/₂ х.

1885.  у  = х² — 5 — 2х — 8х³.                  1890. у = ¹/_√2 х + cos х.

Доказать, что данные функции (№ 1891—1894) являются монотонными на всей числовой прямой. Какие из них монотонно возрастают и какие монотонно убывают?

1891.   у   = ¹/₃ х³ — ¹/₂ х² + х — 5.        1893.  у   = √2 х — cos х.

1892.   у   = 6 — 6х — 2х³ + 3х².           1894.  у   = sin х — ^π/₂ х.

Определить участки возрастания и участки убывания следующих функций:

ОТВЕТЫ