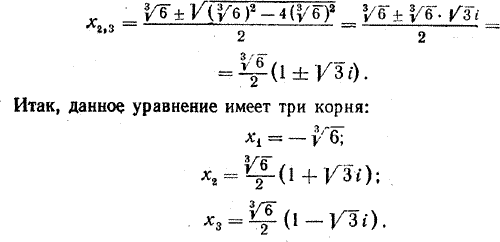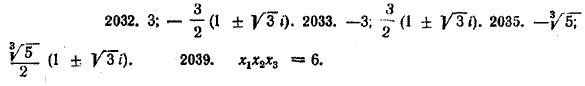КОМПЛЕКСНЫЕ ЧИСЛА     XI

§ 254. Двучленные уравнения 3-й степени с действительными коэффициентами

Так называются уравнения вида

ах³ = b,

где а и b — произвольные действительные числа, отличные от нуля.

Решение таких уравнений мы рассмотрим на некоторых частных примерах.

Пример   1.   Решить уравнение х³ = 8.

Перепишем данное уравнение в виде х³ — 8 = 0. Используя формулу для разности кубов, получим: (х — 2) (х² + 2х + 4) = 0. Если х — 2 = 0, то  х = 2; если же х² + 2х + 4 = 0, то  х = — 1 ± √1—4 = — 1 ± √—3 = r^> = — 1 ± √3 i. Таким образом, данное уравнение имеет три корня:

x₁  = 2;    x₂ = — 1 — √3 i  ;   x₃ = — 1 + √3 i.

Действительным среди них является лишь один корень х = 2

П.р и м е р 2. Решить уравнение  — ¹/₂  х³ = 4.

Умножив обе части этого уравнения на —2, мы придем к уравнению х³ = —8. Это уравнение принципиально не отличается от ранее рассмотренного уравнения х³ = 8. Поэтому мы приводим его решение без объяснений:

х³ + 8 = 0,

(х + 2)(х² — 2х + 4) = 0,  

 x₁ = — 2; x₂ = 1 — √3 i ;  x₃ = 1 + √3 i.

Пример 3.  Решить уравнение ¹/₃ х³  = — 2.

Умножив обе части этого уравнения на 3, получим х³ = — 6, откуда х³ + 6 = 0. Рассматривая число 6 как куб числа ³√6, разложим х³ + 6 на множители:

(х³ + 6) = (х + ³√6) [х² — ³√6 х + (³√6)²].

Следовательно, либо х + ³√6 = 0, либо х² — ³√6 х + (³√6)² = 0. Первое из этих  уравнений имеет корень x₁ = — ³√6.  Второе уравнение дает:

Из этих трех корней лишь один представляет   собой   действительное число.

Упражнения

Решить уравнения  (№2032—2037):

2032.  3х³ = 81.               2034. х³ = 3.             2036. 3х³ = 2.

2033.  х³ = — 27.            2035. х³ = — 5.         2037. — 4х³= ¹/₂

2038.  Доказать, что сумма всех корней уравнения х³ = — 4 равна 0.

2039.  Найти   произведение  всех   корней   уравнения  х³ = 6.

ОТВЕТЫ