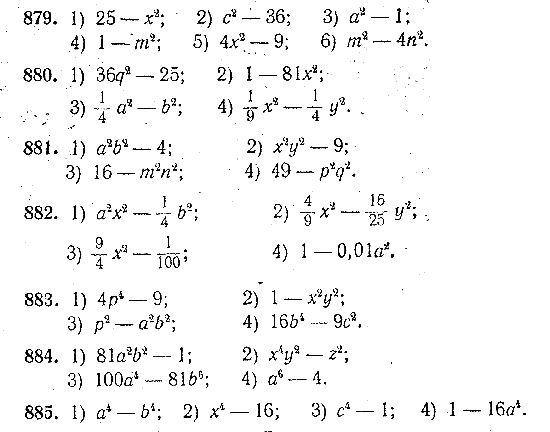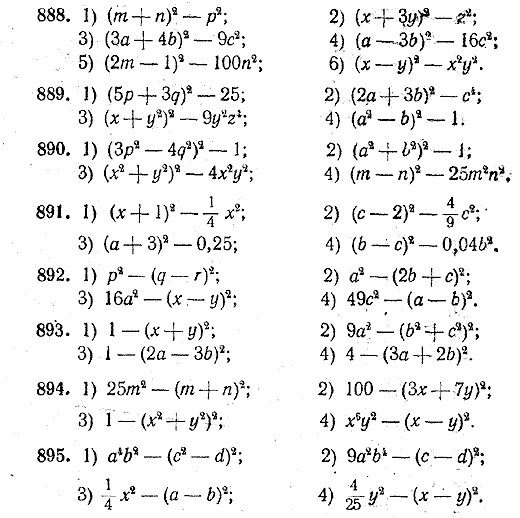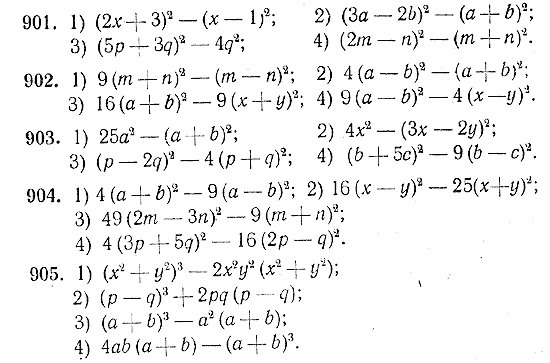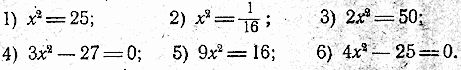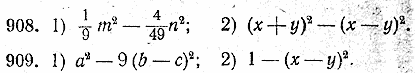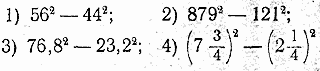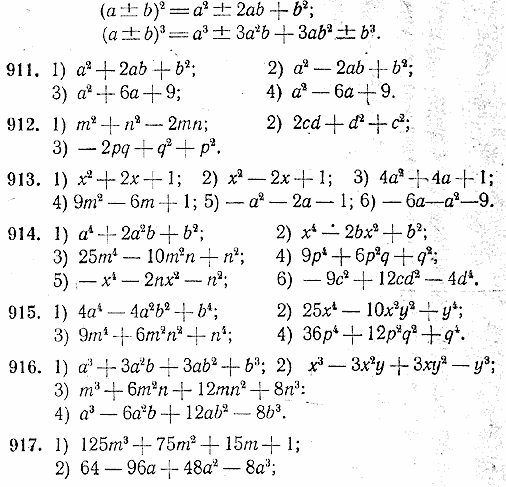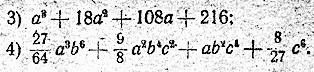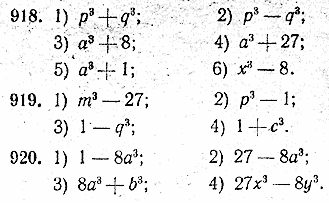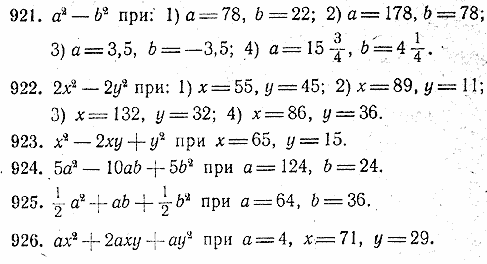ГЛАВА VI

РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ.

§ 28. Разложение на множители по формулам умножения.

№ 873—875 устно.

873.    В   формуле   (а + b) (а — b) = а² — b²    поставить правую часть равенства вместо левой,   а  левую  часть — вместо правой и прочитать получившуюся формулу.

874.  Разложить на множители:

1) x²— y²       2) т² — п²;  

3) а² —4;            4) р² — 9.

875.  Придумать 4 примера на разложение  на множители по формуле разности квадратов двух чисел.

876.  Следующий пример решить двумя способами:

1)  не выполняя преобразований;

2)  разложив предварительно на множители

76² — 24².

Какой способ рациональнее?

877. Вычислить устно, используя разложение  на множители  по формуле разности квадратов чисел:

878. Придумать 4 примера  на  вычисление  с  использованием формулы разности квадратов чисел.

Разложить на множители (№ 879—881 устно):

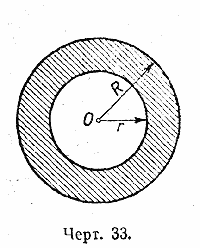
886. Радиус внешнего круга кольца равен R, а радиус внутреннего круга r.

1) Вывести формулу площади S кольца, зная, что площадь круга равна πR²,   где  π ≈ 3,14   (черт. 33).

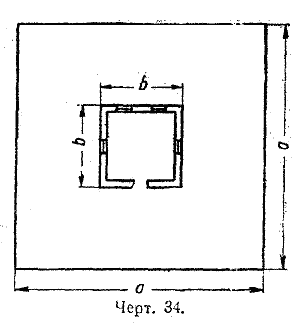
2) Разложить получившееся выражение площади кольца на множители.

3)  Вычислить площадь кольца при

R ≈ 2,5 м,   r ≈ 1,5 м;

R ≈ 4,25 м,    r ≈ 1,25 м;

R= 15,25 см, r = 5,25 см.

887. На чертеже 34 изображён план земельного участка, часть которого занята постройкой,

1) Составить формулу для вычисления площади S незастроенной части участка по размерам, указанным на   плане.

2) Вычислить значение S при  а = 45,5 м,  b =14,5 м.

Разложить на множители:

897*. 1) Доказать, что если а — целoе число, то (2а+1)²—1 делится на 8 без остатка.

2) Привести 3 числовых примера, поясняющих данное свойство целых чисел,   и   сформулировать  это  свойство.

898.   1) Доказать, что разность квадратов двух последовательных чётных чисел делится на 4 без остатка.

2) Привести 3 числовых примера, поясняющих данное свойство чётных чисел.

899.   1) Доказать, что если а — целое число, то а³ — а делится на 6 без остатка.

2) Привести примеры и сформулировать данное свойство.

900.  Зная, что а³ — а, где   а — целое  число,   делится на 6, доказать, что следующие выражения делятся на 6:

а³ +5а ;            а³ +11а;       а³ —19а

Указание:      а³ +5а = а³ — а + 6а =  (а³ — а) + 6а

Разложить на множители:

906. Решить следующие уравнения путём разложения левой части уравнения на множители:

907. Следующие уравнения привести к виду х² — b² = 0 и решить их путём разложения левой части на множители:

Разложить на множители:

910. Вычислить:

Разложить на множители,   используя формулы умножения:

Разложить на множители:

Найти .числовые значения выражений, предварительно разложив их на множители:

ОТВЕТЫ