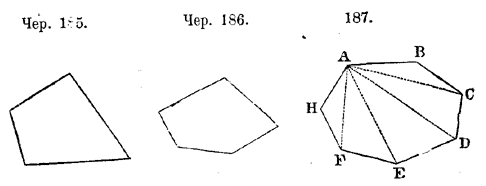
ГЛАВА VI.

О МНОГУГОЛЬНИКАХ.

122. Многоугольником (чер. 185, 186, 187) наз. фигура, ограниченная со всех сторон четырьмя, пятью..., вообще больше чем  тремя прямыми линиями. Сколько сторон в многоугольнике, стодько же в нем и углов; от числа их многоугольники   получают   свои   названия;   на чер. 185-м представлен четырехугольник, на чер. 186-м пятиугольник.

Сумма всех сторон многоугольника наз. его периметром; есди, напр.,имеем четырехуг.,которого одна сторона=3 верш., другая=5 вер., третья=4 в., четвертая = 6 вер., то периметр = 18 вер.

Прямые линии АF, AЕ... (Чер. 187), соединяющия вершины двух углов многоугольника, наз. его диагоналями. Из вершины каждого угла многоугольника можно провести диагонали во все прочие вершины, кроме её самой и двух соседних вершин; след. из каждой вершины многка можно провести столько диагоналей, сколько в многоугольнике сторон без трех; так, в семиуг. (чер. 187) можно провести из  каждой   вершины   четыре диагонали;   в пятиуг. — две и т. д.

123. Диагоналями, проведенными из А (чер. 187), многоуг. АВСDЕFH разделился на тр-ки АВС, АСD, АDE, АЕF, АFН, из которых два крайние состоят каждый из диагонали и двух сторон многоуг.; каждый же из средних имеет своими сторонами две диагонали и одну сторону многоуг.; след. диагонали, проведенныя из каждой вершины   многоугольника, делят его на столько треугольников, сколько в многоуг. сторон без двух; так, шестиуг. разделяется на 4 треуг., десятиуг. на 8, и т. под.

124.  Так как сумма углов каждого тр-ка равна 2 прямым, то след. сумма углов всякого многка будет равна 2 прям., повторенным столько раз, на сколько он разделяется   треугольников; или = двум прямым,   умноженным на число сторон без двух. Так, сумма углов 6-ка=2 пр.• 4=8 пр.=720°.

125.   Если все стороны какого-нибудь   многка (чер. 188) продолжим по одному направлению, то получим углы а, b, с..., наз.    внешними   углами    мног-ка.

Каждый внешний угл. со смежным ему внутренним составляет 2 пр.; след. сумма всех углов, внутренних и внешних, в начерченном мног-ке составляет 12 прям.; но сумма одних внутренних   = 8 прям.; след. сумма внешних  =4 пр. угл.

Если бы вместо 6-ка мы взяли 8-к, то сумма его внутрен. и внешн. уг. равнялась бы 16 пр., а сумма одних внутр.=12 пр , след. сумма внешних углов была бы опять  =4 пр. Вообще—сумма внешних углов всякого многоугольника (сколько бы в нем ни было сторон) равна 4 прямым.

126. Правильные многоугольники. Правильным многоугольником наз. такой, у котораго все стороны и все углы равны между собою.

На чер. 189 изображены правил. 8 к и 6-к. Легко найти, чему равен каждый уг. какого-нибудь прав. мног-ка; для этого нужно сумму углов мног-ка (которую мы уже умеем найти) разделить на число их; так, сумма углов 6-ка = 8 пр., след. каждый уг. прав. 6-ка= ⁸/₆ прям. = ⁴/₃ пр. = 120°; угол прав. 10-ка = ¹⁶/₁₀ d = ⁸/₅d =144°, и т. под. Из этого видно, что чем больше сторон имеет прав. мног-к, тем тупее становятся его внутренние углы и след. тем острее внешние.

127. Вопросы. 1) Что наз. многоуг.? 2) Как разделяются многоуг.? 3) Что наз. периметром мног-ка? 4) Что наз. диагональю? 5) Сколько можно провести диагоналей из каждого угла в 4-ке, 7-ке, 10-ке, 14-ке, 3-ке? 6) На сколько тр-ков можно разделить диагоналями, проведенными из вершины одного угла, 5-к, 8-к, 15-к? 7) Чему равна сумма внутр. угл. 8-ка, 4-ка, 10-ка? 8) Какие углы мног-ка наз. внешними? 9) Чему равна сумма внешн. уг. 5-ка. 3-ка, 8-ка? 10) Какие многки наз. правильными? 11) Чему равен каждый внутр. уг. прав. 8-ка, 4-ка, 10-ка, 18-ка? Чему = каждый внешний уг. прав. 5-ка, 8-ка, 3-ка, 4-ка? 13) Сколько может быть острых углов в четырехугольнике? прямых? тупых? 14) Можно ли начертить 5-к, в котором все углы были бы тупые? 6-к с 6-ю острыми угл.? 8-к с 8-ю прям. уг.?

128. Задачи. 1) Сколько всего диагоналей можно   провести в семиугольнике? в 17-ке? в 24-ке? в тр-ке?

2)  Чему равна сумма внутренних углов 16-ка? 19-ка? 24-ка? 48-ка? 100-ка?

3)  Сколько сторон имеет мног-к, сумма углов которого= 16 прям.? 8d? 360°? 540°? 950°? 12d ? 29d ?

4)  Внешний уг. прав. мн-ка = 40°; сколько сторон в мн-ке?

5)  Внешний уг. прав. мн-ка=45°; определить  сумму внутр. уг-лов?

6)  В каком прав. мн-ке внешний уг. = ¹/₂ внутреннего? ²/₃? ¹/₅? равен внутреннему? вдвое больше внутреннего?

7)  Сторона прав. 6-ка=3 арш.; чему равен периметр?

8)  Определить внутр. и внешний угол прав. 12-ка?прав. 15-ка? прав. 36-ка?

9) Сколько сторон имеет прав. мн-к,внутр. угол которого= =108°? 135°? 175°? 176°24'?  ⁶/₅d? 1,6d?

10)  В каком прав. мн-ке внешний уг.=40°? 22 ¹/₂° ? 12°? 1°? d ? ⁴/₇ d ? 0,4 d ?

11)  В прав. 6-ке АВСDЕF стороны FА и СВ, прилежащиe к стороне АВ, продолжены до пересечения в точке M; какой угол образовался при M?

12)   Сколько сторон имеет мн-к, сумма внутренних углов которoго = 17 d? 2070°?

13)  Три угла 4-ка относятся между собою как 2:5:7; отношение четвертoго угла к третьему=1,(428571); определить углы?

14)  Углы 5-ка относятся между собой как первые пять целых чисел; определить эти углы?

15) В каком мн-ке сумма внутр. углов=сумме внутр. углов 11-ка и 13-ка?

16)  Число диагоналей, которые можно провести из какой-нибудь вершины мн-ка, пятью больше половины числа сторон его; сколько сторон в мн-ке?

17)  Сколько сторон имеет мн-к, если число диагоналей, ко-торые можно провести из каждой его вершины, равно утроенному числу его сторон без 25?

18)  Сумма внутренних углов мн-ка  вместе   с одним из внешних составляет 3956°17'; определить число сторон мн-ка?

19)  На плоскости находятся 18 точек, из которых казкдые три не лежат   на одной прямой линии; сколько   прямых   линий можно провести от каждой точки к остальным?

20)  На данной линии построить помощью   транспортира  прав. 6-к? 5-к? 8-к? 10-к?

21)  На данной прямой линии АВ построить без помощи транспортира прав. 6-к?

22)  Построить мног-к, равный данному?

23)  Доказать, что во всяком мног-ке каждая сторона меньше полупериметра?

ОТВЕТЫ