Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§ 10. ПЕРПЕНДИКУЛЯР К ПРЯМОЙ.
ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА К ПРЯМОЙ
1. Перпендикуляр к прямой.
Основные свойства перпендикуляра.
Прямые линии, образующие между собой прямые углы, называются взаимно перпендикулярными.
Прямые АВ и СD (черт. 54) взаимно перпендикулярны.
Перпендикулярность прямых обозначается знаком _|_. На чертежах 53 и 54 АВ_|_DС и DС _|_ АВ.
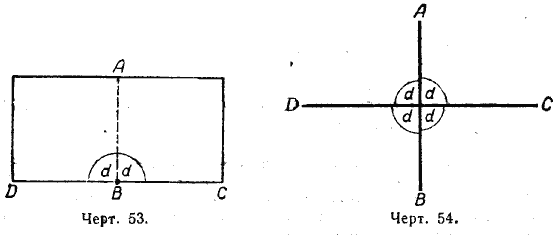
Каждая из этих прямых называется перпендикуляром к другой. АВ — перпендикуляр к СD, и СD — перпендикуляр к АВ.
К данной прямой через данную на ней точку можно провести, только один перпендикуляр (черт. 55).

В самом деле, если АВ_|_СD, то всякая другая прямая, проведённая через точку О прямой СD, например LК, не будет перпендикулярна к ней, так как углы КОС и КОD не будут прямыми углами, а один из них будет больше прямого угла, другой меньше.
Точно так же можно провести только один перпендикуляр к данной прямой АВ через точку О и в том случае, когда точка О лежит не на прямой АВ, а вне её (черт. 56).
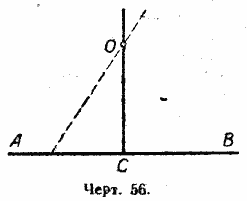
Если ОС_|_АВ, то всякая другая прямая, проходящая через точку О, уже не будет перпендикулярна к прямой АВ. Доказательство этого утверждения будет дано позднее.
2. Построение перпендикуляра к прямой.
Для вычерчивания прямых углов употребляется угольник, или чертёжный треугольник (черт. 57). Прямой угол может быть изображён в любом положении (черт. 58).
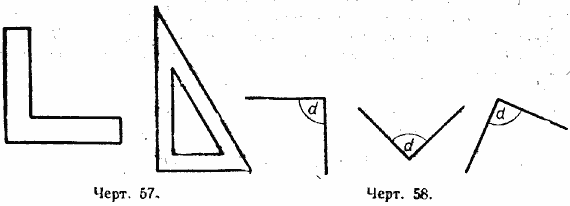
Проведение перпендикуляра к данной прямой А В с помощью чертёжного треугольника через точку О, данную на самой прямой АВ, показано на чертеже 59.

На чертеже 60 показано проведение перпендикуляра к прямой АВ через точку О, данную вне этой прямой.
3. Проверка чертёжного треугольника.
Чтобы проверить чертёжный треугольник, надо начертить прямую линию, взять на ней какую-нибудь точку и, приняв луч за сторону угла, построить при помощи треугольника прямой угол с вершиной в данной точке. Затем чертёжный треугольник надо перевернуть, приложить той же стороной прямого угла к этой прямой в противоположном направлении от вершины и построить второй прямой угол с вершиной в той же точке. Если начерченные прямые совпадут (черт. 61), то чертёжный треугольник верен, если же не совпадут, то треугольник не верен (черт. 62).

4. Углы острый и тупой. Углы, большие развёрнутого.
Так как все прямые углы равны между собой, то прямой угол может быть принят за меру углов.
Угол, меньший прямого, называется острым углом (черт. 63).
Угол, больший прямого, но меньший развёрнутого, называется тупым (черт. 64).

Могут быть углы и большие развёрнутого (черт. 65). Однако мы ограничимся рассмотрением только тех углов, которые меньше развёрнутого; углы же, большие развёрнутого, мы рассматривать не будем, кроме тех случаев, когда это будет особо оговорено.
5. Эккер.
|
Для построения прямых углов на земной поверхности применяется особый прибор, который называется эккером. Эккер представляет собой два бруска, укреплённых под прямым углом. На концах брусков ставятся булавки или тонкие гвозди так, чтобы прямые, соединяющие их (черт. 66), были взаимно перпендикулярны. Эккер укрепляется на треножнике или на палке. Чтобы построить на земле прямой угол, надо наметить вершину угла, а эккер поместить так, чтобы точка пересечения взаимно перпендикулярных прямых (на чертеже они изображены пунктиром) оказалась на одной отвесной линии с намеченной вершиной угла на местности. Затем по направлению булавок одного бруска провешить одну прямую линию, а по направлению булавок второго бруска — вторую прямую (черт. 67). |
|

Если надо провести прямую, перпендикулярную к данной прямой в данной точке, то эккер ставится над этой точкой так, чтобы направление булавок одного бруска совпадало с направлением данной прямой. Затем по направлению другого бруска провешивается вторая прямая, которая с данной прямой образует прямой угол, т. е. перпендикулярна к ней.
Упражнения.
1. Начертить прямую, взять на ней точку и провести с помощью чертёжного треугольника перпендикуляр к данной прямой через данную точку.
2. Начертить прямую, взять точку вне этой прямой и с помощью чертёжного треугольника провести к прямой перпендикуляр, проходящий через данную точку.
3. Назвать все углы, которые имеются на чертежах 68 и 69 (не считая углов, которые больше развёрнутого).

4. Вырезать из плотной бумаги квадрат. Разрезать его на две равные части, как показано на чертеже 70, и из полученных двух фигур составить фигуры, изображённые на чертеже 71, а, б, в, г, д, е, ж, э.

