Г Л А В А I.

ОСНОВНЫЕ ПОНЯТИЯ.

§ 12. ОКРУЖНОСТЬ.  КРУГ.

1. Радиус. Хорда. Диаметр.

Если мы раскроем циркуль и укрепим конец одной ножки в какой-нибудь точке плоскости, а другую ножку будем вращать, не меняя раствора циркуля, так, чтобы её конец двигался по плоскости (черт. 82), то этот конец опишет кривую линию, все точки которой находятся на равном расстоянии от одной и той же точки. Если вращение продолжать до тех пор, пока кривая окажется замкнутой, то получим о к р у ж н о с т ь.

Окружностью называется кривая замкнутая линия на плоскости, все точки которой находятся на одинаковом расстоянии от одной точки; эта точка называется центром окружности.

Часть плоскости, ограниченная окружностью, называется кругом (черт. 83).

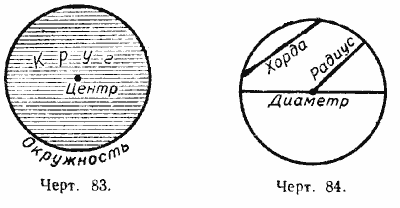
Отрезок прямой, соединяющий точку окружности с её центром, называется радиусом (черт. 84).

Так как все точки окружности находятся от центра на одном и том же расстоянии, то все радиусы одной и той же окружности равны между собой. Радиус обыкновенно обозначается буквой R или r.

Точка, взятая внутри окружности, находится от её центра на расстоянии, меньшем радиуса. В этом легко убедиться, если через данную точку провести радиус (черт. 85).

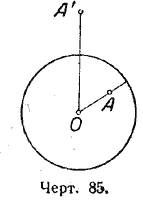
Точка, взятая вне окружности, находится от её центра на расстоянии, большем радиуса. В этом легко убедиться, если соединить данную точку с центром окружности (черт. 85).

Отрезок прямой,   соединяющий  две  точки окружности, называется хордой.

Хорда, проходящая через центр, называется диаметром (черт. 84). Диаметр обыкновенно обозначается буквой D. Диаметр равен двум радиусам:

D = 2r.

Так как все радиусы одного и того же круга равны между собой, то и все диаметры данного круга равны между собой.

Теорема. Хорда, не проходящая через центр круга, меньше диаметра, проведённого в том же круге.

В самом деле, если проведём какую-нибудь хорду, например АВ, и соединим её концы с центром О (черт. 86), то увидим, что хорда АВ меньше ломаной линии АО + ОВ, т. е. АВ < 2r, а так как 2r = D, то АВ < D.

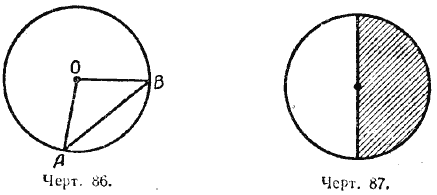
Если круг перегнуть по диаметру (черт. 87), то обе части круга и окружности совместятся. Диаметр делит круг и окружность на две равные   части.

Два круга (две окружности) называются равными, если их можно наложить друг на друга так, чтобы они совместились.

Поэтому два круга (две окружности) с равными радиусами равны.

2. Дуга окружности.

Часть окружности называется дугой.

Слово «дуга» иногда заменяется знаком  .  Дуга обозначается двумя или тремя буквами, из которых две ставятся на концах дуги, а третья — у какой-нибудь точки дуги. На чертеже 88 обозначены две дуги: АСВ и ADB.

В том случае, когда дуга меньше полуокружности, она обычно обозначается двумя буквами. Так, дугу АDВ можно обозначить АВ (черт. 88). О хорде, которая соединяет концы дуги, говорят,  что она стягивает дугу.

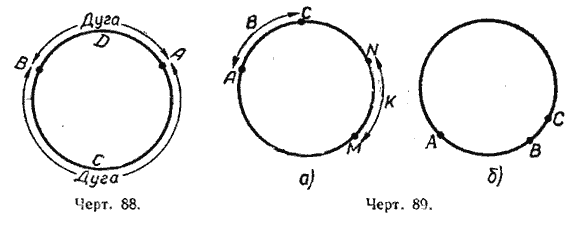
Если передвинуть дугу АС (черт. 89, а) так, чтобы она скользила поданной окружности, и если при этом она совпадает с дугой МN, то АС = NM.

На чертеже 89, б дуги АС и АВ не равны между собой. Начинаются обе дуги в точке А, но одна дуга  ( АВ) составляет только часть другой дуги (AС).  
Поэтому    АС > АВ;     АВ < АС.

Упражнения.

1. Сформулируйте определения, которые приведены в данном параграфе.

2. Сформулируйте теоремы, которые доказаны в данном параграфе.