ГЛАВА II.

ТРЕУГОЛЬНИКИ.

§ 20. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА
ПО ДВУМ ДАННЫМ ЕГО СТОРОНАМ И УГЛУ МЕЖДУ НИМИ.
ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ.

Пусть требуется построить треугольник, одна сторона которого равна, например,
35 мм, другая сторона равна 32 мм и угол, заключённый между этими сторонами, равен 46°.

Построим с помощью транспортира /  A, равный 46°, и на его сторонах отложим отрезки АВ и АС, соответственно равные 35 мм и 32 мм (черт. 143). Соединив точки В и С, получим искомый треугольник ABC.
По тем же данным построим другой треугольник —    /\ А'В'С'.

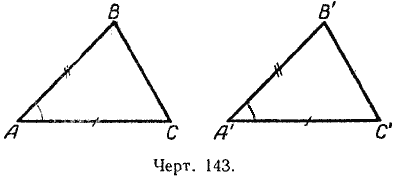
Докажем, что эти треугольники равны между собой.
Для этого наложим /\ А'В'С на /\ AВС так, чтобы вершины А' и А совместились. Сторону А'С' направим по стороне АС. Тогда точка С совместится с точкой С', потому что  А'С' = АС.

Сторона А'В' пойдёт по стороне АВ, так как /  A' = /  A. Точка В' совместится с точкой В, так как А'В' = АВ. Если точки С и С', В и В' совместились, то совместятся и стороны В'С' и ВС.

Треугольники ABC и А'В'С' совпали, значит, они равны.

Мы можем по этим же данным построить сколько угодно треугольников, и все они будут равны между собой.

Таким образом, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольника равны между собой.

Назовём это первым признаком равенства треугольников.