ГЛАВА II.

ТРЕУГОЛЬНИКИ.

§ 27. РАВЕНСТВО ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ.

1. Первые два признака равенства прямоугольных треугольников.

Мы установили, что для равенства двух треугольников достаточно, чтобы три элемента одного треугольника были равны соответствующим элементам другого треугольника, при этом непременно в число этих элементов должна входить хотя бы одна сторона.

Так как все прямые углы равны между собой, то прямоугольные треугольники уже имеют по одному равному элементу, именно по одному прямому углу.

Отсюда следует, что прямоугольные треугольники равны:
   если катеты одного треугольника соответственно равны катетам другого треугольника (черт. 153);
  если катет и прилежащий острый угол одного угольника соответственно равны катету и прилежащему острому углу другого треугольника (черт. 154)..

Упражнения.

Можно ли построить треугольник по стороне и двум углам, если оба заданных угла будут прямые? оба тупые? один прямой, другой тупой?

2.Построить треугольник по трём его сторонам, если его стороны соответственно равны:

а) 6 см, 5 см. 7 см;

б) 5 см, 7 см, 8 см.

3. Можно ли построить треугольник, если стороны его будут соответственно равны

а) 10 см, 6 см, 4 см;

б) 48 мм, 32 мм, 8 мм?

Если нельзя построить эти треугольники, то почему?

4. Построить прямоугольный треугольник с помощью циркуля и чертёжного треугольника по двум его катетам.

2. Две задачи на построение прямоугольных треугольников.

Задача  1.  Построить прямоугольный треугольник по следующим данным:
гипотенуза с = 5,4 см, /  A = 38°.

Решение  (черт. 155).

1.На прямой MN откладываем отрезок АВ = 5,4 см.

2.Строим угол КАВ, равный 38°.

3. Из точки В опускаем с помощью чертёжного треугольника перпендикуляр ВС на прямую АК.

Треугольник АВС отвечает условию задачи.

Задача 2.   Построить прямоугольный треугольник по следующим данным: гипотенуза с = 38 мм, катет b = 26 мм.

Решение (черт. 156).

1. На произвольной прямой МN берём точку С и проводим СК _|_ МN.

2. На прямой СК откладываем отрезок СА = 26 мм.

3. Из точки А, как из центра, радиусом, равным отрезку с= 38 мм, описываем дугу так, чтобы она пересекла прямую МN например, в точке В.

4. Точки А и В соединяем отрезком.  

Треугольник ABC отвечает условию задачи.

Докажем теперь две теоремы, устанавливающие ещё два признака равенства прямоугольных треугольников.

3. Теорема о признаках равенства прямоугольных треугольников.

Теорема 1. Если гипотенуза и острый угол одного треугольника   соответственно   равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.

Чтобы доказать эту теорему, построим два прямоугольных гольника ABC и А'В'С', у которых углы А и А' равны, гипотенузы АВ и А'В' также равны, а углы С и С' — прямые (черт. 157).

Наложим треугольник А'В'С' на треугольник ABC так, чтобы вершина А' совпала с вершиной А, гипотенуза А'В' — с равной гипотенузой АВ. Тогда вследствие равенства углов A и А' катет А'С' пойдёт по катету АС; катет В'С' совместится с катетом ВС: оба они перпендикуляры, проведённые к одной прямой АС из одной точки В (§ 26,следствие 3). Значит, вершины С и С' совместятся.

Треугольник ABC совместился с треугольником А'В'С'.
Следовательно, /\ АВС = /\ А'В'С'.

Эта теорема даёт 3-й признак равенства прямоугольных треугольников (по гипотенузе и острому углу).

Теорема 2. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные угольники равны.

Чтобы доказать это, построим два прямоугольных треугольника АВС и А'В'С', у которых углы С и С' — прямые, катеты АС и A'C' равны,  гипотенузы АВ и А'В' также равны (черт. 158).

Проведём прямую MN и отметим на ней точку С, из этой точки проведём перпендикуляр СК к прямой MN. Затем прямой угол треугольника ABC наложим на прямой угол КСМ так, чтобы вершины их совместились и катет АС пошёл по лучу СК, тогда катет ВС пойдёт по лучу СМ. Прямой угол треугольника А'В'С' наложим на прямой угол KCN так, чтобы вершины их совместились и катет А'С' пошёл по лучу СК, тогда катет С'В' пойдёт по лучу CN. Вершины А и А' совпадут вследствие равенства катетов АС и А'С'.

Треугольники АВС и А'В'С' составят вместе равнобедренный треугольник ВАВ', в котором АС окажется высотой и биссектрисой, а значит и осью симметрии треугольника ВАВ' ( §  18 ). Из этого следует, что /\ АВС = /\ А'В'С'.

Эта теорема дает 4-й признак равенства прямоугольных треугольников ( по гипотенузе и катету).

4. Перпендикуляр к отрезку, проведённый через его середину.

Теорема. Всякая тонка, лежащая на перпендинкуляре к отрезку, проведённому через его середину, одинакаково удалена от концов этого отрезка (черт. 159).

Пусть прямая ЕО перпендикулярна к отрезку АВ и АО = ОВ. Возьмём на ЕО произвольную точку К и докажем, что АК = КВ.

Прямоугольные треугольники АОК и ВОК равны по двум катета АО = ОВ по условию, КО — общая сторона. Следовательно, АК = ВК. Так как точка К взята произвольно, то и всякая другая точка перпендикуляра ЕО одинаково удалена от концов отрезка АВ.

Если же мы возьмём какую-нибудь точку Р на плоскости, не находящуюся на перпендикуляре ЕО, то отрезки РА и РВ не будут равны (черт. 160).

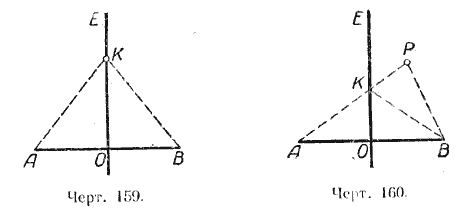
Соединим точку К (точку пересечения ЕО и АР с точкой В. ВК + КР > РВ, но по доказанному ранее АК = ВК, поэтому АК + КР > РВ, или АР>РВ, т. е. всякая точка, не находящаяся на перпендикуляре ЕО, неодинаково удалена от концов отрезка АВ.

Упражнения.

1. Построить равносторонний треугольник по дайной его стороне.

2. В следующих задачах дополнить условие недостающими данными, чтобы решение каждой задачи было единственным:

а) Построить равнобедренный треугольник по данному его основанию.

б) Построить прямоугольный треугольник по данному его катету,

в) Построить прямоугольный треугольник по данной  его гипотенузе;