ГЛАВА IV.

ЧЕТЫРЁХУГОЛЬНИКИ.

§ 48. СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА

Теорема. Отрезок,соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника и равен ее половине.

Дано: в треугольнике АВС   АМ = ВМ и СК = ВК. Надо доказать:   
 1) МК || АС;
 2) МК = ^AC/₂ .

Доказательство. Продолжим МК на отрезок КЕ = МК и точку С соединим с точкой Е (черт. 251).

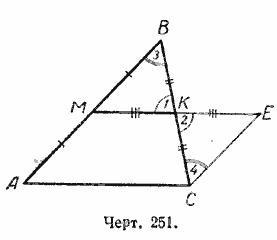
Рассмотрим треугольники МВК и КЕС.

СК = КВ — по условию,
 КЕ = МК — по построению,
/   1 = /   2, как вертикальные
Следовательно /\  МВК =  /\ КЕС

Из равенства этих треугольников следует:
1) ЕС = МВ и, значит, ЕС = АМ;
2) /  4 = /  3, но это углы внутренние накрест лежащие при прямых ЕС и МВ и секущей ВС, следовательно, ЕС || МВ и, значит, ЕС || АМ.

Рассмотрим теперь четырёхугольник АМЕС. В нем ЕС = АМ и ЕС || АМ, поэтому
АМЕС — параллелограмм (§ 43, п. 3).

Из этого cледует:

 1) МЕ || АС и, значит, МК ||АС,
 2) МЕ = AС и, значит, МК = ^AC/₂

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

Упражнения.

1. Доказать, что прямая, проходящая через середину какой-либо стороны треугольника параллельно другой его стороне, делит третью сторону треугольника пополам.

2. Доказать, что отрезки, соединяющие последовательно середины сторон любого четырёхугольника, образуют параллелограмм.

Указание.  Провести в четырёхугольнике диагонали.

3. Диагонали четырёхугольника равны 38 мм и 36 мм. Вычислить периметр параллелограмма, образованного отрезками, соединяющими середины сторон этого четырёхугольника.