ГЛАВА IV.

ЧЕТЫРЁХУГОЛЬНИКИ.

§ 49. ТРАПЕЦИЯ.

Четырёхугольник, у которого две противоположные стороны параллельны, а другие две не параллельны, называется трапецией.

На чертеже 252 у четырёхугольника АВDС АВ || СD,  AC || BD.  АВDС — трапеция.

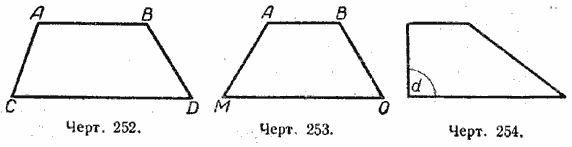
Параллельные стороны трапеции называются её основаниями;  АВ и СD — основания трапеции. Остальные две стороны называются боковыми сторонами трапеции; АС и ВD — боковые стороны трапеции.

Если боковые стороны равны, то трапеция называется равнобедренной.

Трапеция АВОМ равнобедренная, так как АМ=ВО (черт. 253).

Трапеция, у которой одна из боковых сторон перпендикулярна к основанию, называется прямоугольной (черт. 254).

Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.

Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.

Дано: ОС — средняя линия трапеции АВDК, т. е. ОК = ОА и ВС = СD (черт. 255).

Надо доказать:

1) ОС || КD и ОС || АВ;
 2)

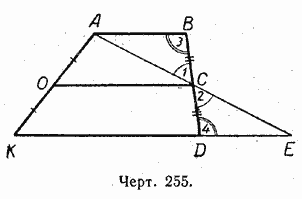
Доказательство. Через точки А и С проведём прямую, пересекающую продолжение основания КD в некоторой точке Е.

В треугольниках АBС и DСЕ:
ВС = СD — по условию;
/  1 = /  2, как вертикальные,
/  4 = /  3, как внутренние накрест лежащие при параллельных АВ и KЕ и секущей ВD. Следовательно, /\ АBС = /\ DСЕ.

Отсюда АС = СЕ, т.е. ОС является средней  линией треугольника КАЕ. Следовательно (§ 48):

 1) ОС || КЕ и, значит, ОС || КD и ОС || AВ;
 2) , но DЕ = АВ (из равенства треугольников АBС и DСЕ), поэтому отрезок DЕ можно заменить равным ему отрезком АВ. Тогда получим:

Теорема доказана.

Упражнения.

1. Доказать, что сумма внутренних углов трапеции, прилежащих к каждой боковой стороне, равна 2d.

2. Доказать, что углы при основании равнобедренной трапеции равны.

3. Доказать, что если углы при основании трапеции равны, то эта трапеция равнобедренная.

4. Доказать, что диагонали равнобедренной трапеции равны между собой.

5. Доказать, что если диагонали трапеции равны, то эта трапеция равнобедренная.

6. Доказать, что периметр фигуры, образованной отрезками, соединяющими середины сторон четырёхугольника, равен сумме диагоналей этого четырёхугольника.

7. Доказать, что прямая, проходящая через середину одной из боковых сторон трапеции параллельно её основаниям, делит другую боковую сторону трапеции пополам.