ГЛАВА VII.

ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.

§ 70. ДИАМЕТР, ПЕРПЕНДИКУЛЯРНЫЙ К ХОРДЕ.

Теорема 1.  Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.

Пусть диаметр АВ перпендикулярен к хорде СD (черт. 312). Требуется доказать, что
СЕ = ЕD, СВ = ВD, СА = DА.

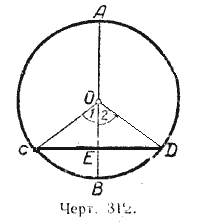
Соединим точки С и D с центром окружности О. В равнобедренном треугольнике
СОD отрезок ЕО является высотой, проведённой из вершины О на основание СD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и / 1 = / 2. Но / 1 и / 2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно
СВ = ВD. Дуги СА и ВА также равны между собой, как дополняющие равные дуги до полуокружности.

Теорема  2 (обрaтная). Диаметр,   проведённый   через   середину хорды, не проходящей через центр, перпендикулярен к ней и делит дуги, стягиваемые хордой, пополам.

Пусть диаметр АВ делит хорду СD пополам. Требуется доказать, что АВ_|_СD,
СВ = ВD и СА = АВ (черт. 313).

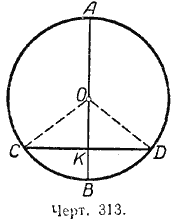
Соединим точки С и В с центром круга. Получим равнобедренный треугольник СОD,    в котором ОК   является медианой, а значит, и высотой. Следовательно, АВ_|_СD,   а  отсюда (по теореме   1) следует,   что СА = АD; СВ = ВD .    

Теорема 3 (обратная).Диаметр, проведённый  через середину дуги, делит пополам хорду,  стягивающую эту дугу, и перпендикулярен к этой хорде.

Пусть диаметр АВ делит дугу СВD пополам (черт. 313). Требуется доказать, что
СК = КD и АВ _|_ СD.

Соединим центр круга О с точками С и D. В равнобедренном треугольнике СОD отрезок ОК является биссектрисой угла СОD, так как по условию теоремы СВ = ВD, поэтому ОК будет и медианой и высотой этого треугольника. Следовательно, диаметр АВ проходит через середину хорды и перпендикулярен к ней.