ГЛАВА VII.

ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.

§ 73. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ.

1. Возможны следующие три случая взаимного положения прямой и окружности:

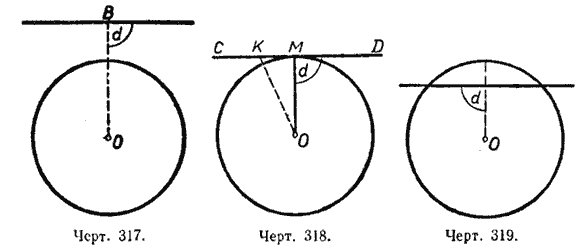
1) Прямая не имеет с окружностью ни одной  общей   точки (черт. 317).

2) Прямая с окружностью имеет только    одну общую точку (черт. 318).

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.

3) Прямая имеет с окружностью две общие точки (черт. 319). Такая прямая называется секущей.

2. Теоремы о касательной к окружности.

Теорема 1. Прямая, перпендикулярная к радиусу в конечной его точке, лежащей на окружности, является касательной к окружности.

Пусть ОМ— радиус окружности, СD_|_OМ (черт. 318).

Требуется доказать, что СD— касательная к окружности.

Доказательство. Если ОМ _|_СD, то расстояние от центра О до любой другой точки прямой СD больше радиуса ОМ, следовательно, всякая точка прямой СD, кроме точки М, лежит вне круга. Поэтому точка М — единственная общая точка прямой СD и окружности, а это означает, что СD— касательная к окружности.

Теорема 2 (обратная). Касательная к окружности перпендикулярна к радиусу этой окружности, проведённому в точку касания.

Пусть прямая СD — касательная к окружности и М — точка касания.

Требуется доказать, что СD _|_ ОМ (черт. 318).

Доказательство. Если прямая СD касается окружности в точке М, то всякая другая точка прямой СD будет находиться вне круга, ограниченного этой окружностью, следовательно, расстояние от каждой точки прямой СD до центра, кроме точки М, будет больше расстояния ОМ — радиуса окружности. Значит, этот радиус есть наименьший из отрезков, соединяющих точку О с точками прямой СD, поэтому ОМ _|_ СD.

3. Свойство дуг, заключённых между касательной и параллельной ей хордой.

Теорема. Дуги, заключённые между касательной и параллельной ей хордой, равны.

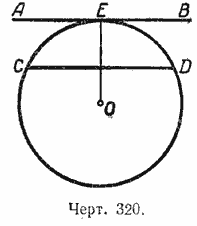
Пусть касательная АВ и хорда СD параллельны. Точка Е — точка касания прямой АВ с окружностью О (черт. 320).

Требуется доказать, что СЕ = ЕD.

Для доказательства соединим точку касания Е с центром круга.

ОЕ _|_АВ, а так как СD || АВ, то ОЕ _|_ СD, а перпендикуляр к хорде, проведённый из центра той же окружности, делит стягиваемую ею дугу пополам.
Следовательно, СЕ = ЕD.

4. Построение касательной к окружности.

Задача. Построить прямую, касательную к окружности в данной её точке.

Дана окружность О, требуется провести прямую, касательную к этой окружности в точке М (черт. 321).

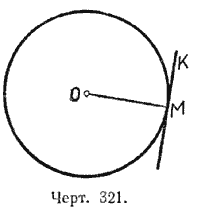
Проведём радиус ОМ и через конечную его точку М проведём прямую КМ, перпендикулярную к радиусу. По доказанному ранее прямая КМ будет касательной к окружности.