ГЛАВА IX.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОСТРОГО УГЛА.
§ 101. ПРАКТИЧЕСКИЕ ЗАДАЧИ С ПРИМЕНЕНИЕМ ТРИГОНОМЕТРИИ.
Знание тригонометрических функций позволяет нам решать практические задачи более совершенными методами и с большей точностью. Рассмотрим несколько таких задач.
1. Определить высоту предмета, к основанию которого подойти нельзя.
Например, нужно определить высоту телевизионной антенны, которая отделена от нас рекой (черт 403).
Рассмотрим прямоугольный треугольник ACD. В этом треугольнике мы можем с помощью астролябии измерить угол А. Положим, он равен 42°.
Черт 403
В тpeyгольнике BCD измеряем / DBC, пусть он равен 47°.
Решение.
; 
(точки A, B, С находятся на одной прямой)
Расстояние АС — ВС, т. е. АВ, может быть непосредственно измерено, пусть оно равно 12,0 м, тогда
12,0 = CD(1,1106 — 0,9325) = CD• 0,1781.
Откуда 
Для окончательного определения высоты антенны к 67,4 м следует прибавить высоту прибора, с помощью которого определяли углы А и В. Если высота прибора, например, составляла 1,40 м, то окончательно высота антенны будет равна 67,4 + 1,40 = 68,8 (м).
2. Определить расстояние между пунктами А и В, разделёнными препятствием.
а) Пусть требуется найти расстояние от пункта А до пункта В, находящегося за рекой
(черт.404) .
Черт.404
Строим при помощи астролябии или эккера при точке А прямой угол ВАС, Взяв на прямой АС произвольную точку D, с помощью астролябии измеряем угол ADB; пусть он равен 44°. Измеряем расстояние AD; пусть оно составит 120 м.
Тогда 
, или АВ = 120•tg 44o 
120 • 0,9657 116 (м).
б) Пусть нужно определить расстояние от пункта А до пункта В, между которыми находится водное пространство (черт. 405).
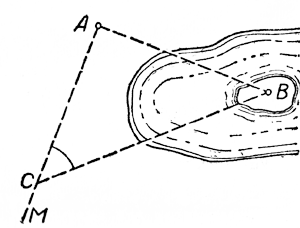
Черт. 405
Принимая точку А за вершину угла, строим прямой угол ВАМ. На прямой AM фиксируем какую-нибудь точку С, находящуюся от точки А на расстоянии, например, 200 м. С помощью астролябии определяем угол АСВ. Пусть он будет равен 48°. Тогда
или 
Откуда АВ = 1,1106• 200 222 (м).
Практические работы
1. Определить в окружающей обстановке высоту какого-нибудь предмета, к основанию которого подойти нельзя.
2. Определить расстояние до какой-нибудь недоступной точки.