ГЛАВА II.

ТРЕУГОЛЬНИКИ.

§ 7. Понятие о многоугольнике. Треугольник и его элементы.

Многоугольник.

118. Начертить выпуклые четырёхугольник и пятиугольник и провести в них все диагонали. Сколько диагоналей имеет каждый из этих многоугольников?

119. 1) На сколько треугольников делится выпуклый пятиугольник диагоналями, проведенными из одной его вершины? Решить эту задачу для семиугольника и восьмиугольника.

2) Выразить в общем виде число треугольников, на которые делится выпуклый n-угольник диагоналями, проведёнными из одной его вершины.

120. Доказать, что два внешних угла многоугольника, построенные при одной из его вершин, равны.

Треугольник и его элементы.

121. Перечислить все треугольники, изображённые на чертежах 36 и 37.

122. На чертеже 38 изображены восемь треугольников. Укажите вид каждого треугольника.

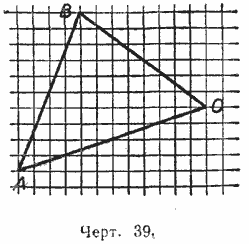
123. 1) Перечертить в тетрадь по клеточкам треугольник ABC (черт. 39) и провести в нём все высоты. Измерить их.

2) Перечертить в тетрадь по клеточкам треугольник АВС (черт. 39), провести в нём все медианы и измерить их.

3) Перечертить в тетрадь по клеточкам треугольник ABC (черт. 39), провести в нём все биссектрисы и измерить их.

124. 1) Начертить треугольник с прямым углом и провести в нём из вершины острого угла высоту, медиану и биссектрису.

2) Начертить треугольник с тупым углом и провести в нём из вершины острого угла высоту, медиану и биссектрису.

125*. Вершина А остроугольного треугольника ABC находится вне чертежа. Найти основание высоты треугольника ABC, проходящей через вершину А. (Задачи, отмеченные звёздочкой, повышенной трудности.).

126. Перечертить в тетрадь отрезок АВ и точку М, данные на чертеже 40.

Построить треугольник ABC, считая отрезок АВ стороной искомого треугольника, а точку М: а) точкой пересечения его высот, б) точкой пересечения его биссектрис.

127. Доказать, что медиана, проведённая к основанию равнобедренного треугольника, делит его на два треугольника, периметры которых равны.

128. Через вершину равнобедренного треугольника, основание и боковая сторона которого соответственно равны 10 см и 13 см, проведена медиана. Найти её длину, если известно, что периметр одного из образовавшихся треугольников равен 30 см.

ОТВЕТЫ