ГЛАВА III.

ПАРАЛЛЕЛЬНОСТЬ.

§ 13. Углы с соответственно параллельными и перпендикулярными сторонами.

Углы с соответственно параллельными сторонами.

286. При помощи чертёжного треугольника и линейки построить:
а) угол с вершиной в данной точке, равный данному;
б) угол с вершиной в данной точке, дополняющий данный до 180°.

287. Построить два угла с соответственно параллельными сторонами так, чтобы:
а) эти углы были равны; б) один из углов был острый, а другой тупой.

288. Даны два угла с соответственно параллельными сторонами. Найти эти углы, если: а) один из них в четыре раза меньше другого; б) один из них больше другого на 35°.

289. Два угла с соответственно параллельными сторонами относятся, как 2:7. Определить эти углы.

290. 1) Как найти величину угла между двумя непараллельными прямыми, точка пересечения которых находится вне чертежа?

2) Как найти величины углов треугольника, если на чертеже даны лишь направления сторон, а вершины треугольника находятся вне чертежа?

291. 1) Две прямые образуют углы, один из которых равен 82°. Через точку, взятую внутри большего угла, проведены прямые, параллельные данным прямым. Определить меньший из углов, образованных проведёнными прямыми.

2) Внутри угла, равного 56°, взята точка и через неё проведены прямые, параллельные сторонам этого угла. Найти углы полученного четырёхугольника.

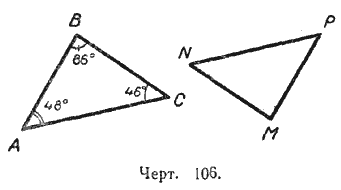
292. В треугольниках ABC и MNP — три пары соответственно параллельных сторон (черт. 106). Найти углы треугольника MNP по данным углам треугольника ABC.

Углы с соответственно перпендикулярными сторонами.

293. 1) Построить угол с вершиной в данной точке, равный данному.

2) Построить угол с вершиной в данной точке, дополняющий данный угол до 180°.

294. Построить два угла с соответственно перпендикулярными сторонами так, чтобы: а) эти углы были равны; б) один из этих углов был острый, а другой тупой.

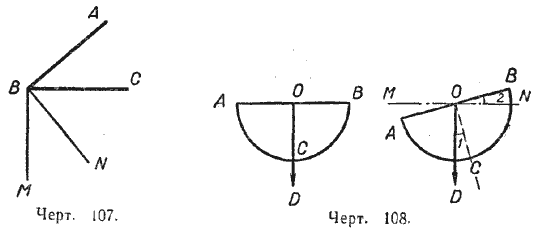
295. Дан угол ABC, равный 40°. Из вершины угла проведены лучи ВМ и BN, перпендикулярные сторонам данного угла (черт. 107). Найти величины углов NBM, АВМ и CBN.

296. Даны два угла с соответственно перпендикулярными сторонами. Определить эти'углы, если: а) один из них больше другого в пять раз; б) один из них меньше другого на 24°.

297. Два угла с соответственно перпендикулярными сторонами относятся, как 17 : 19. Определить эти углы.

298. Две прямые образуют углы, один из которых равен 36°. Через точку, взятую внутри меньшего угла, проведены прямые, перпендикулярные данным прямым. Определить меньший из углов, образованных проведёнными прямыми.

299. На чертеже 108 даны изображения двух положений эклиметра, сделанного из обычного классного транспортира (ОD — отвес). Доказать, что /  1 = /  2.

300. Точки А и В, лежащие на сторонах прямого угла С, соединены отрезком прямой. Из вершины прямого угла С к отрезку АВ проведён перпендикуляр CD (точка D лежит на отрезке АВ). Какие из полученных углов составлены соответственно перпендикулярными прямыми?

301. 1) Отрезки BD и CF являются высотами треугольника ABC (черт. 109). Доказать, что /  1 = /  2.

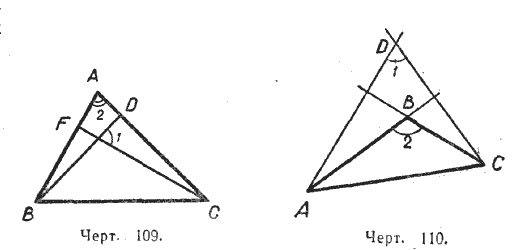
2) AD и CD — прямые, перпендикулярные сторонам ВС и АВ треугольника ABC
(черт. 110). Доказать, что /  1 +  /   2 = 180°.

ОТВЕТЫ

288. а) 36° и 144°; б) 72°30' и 107°30'. 289. 40° и 140°. 291. 1) 82°; 2) 56°, 124°, 56°, 124°. 292. 86°, 48°, 46°. 295. 40°, 130°, 50°. 296. а) 30° и 150°; б) 78° и 102°. 297. 85° и 95°. 298. 36°.