ГЛАВА IX.

ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ.
ПОДОБИЕ ФИГУР.

§ 28. Подобие многоугольников.

841. Какие условия должны выполняться, чтобы были подобны:
а) два прямоугольника; б) два ромба; в) два параллелограмма; г) две равнобедренные трапеции; д) две прямоугольные трапеции?

842. Будут ли подобны два четырёхугольника ABCD и A₁B₁C₁D₁ если будет выполнено только одно из следующих условий:

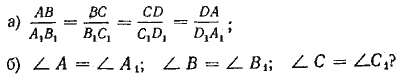
Начертить два четырёхугольника, у которых выполнялось бы только одно из приведённых выше условий.

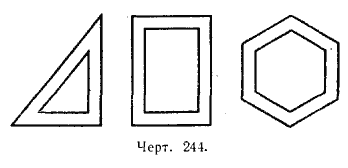
843. На чертеже 244 изображены чертёжный треугольник, рамки прямоугольной и шестиугольной формы; у каждого шестиугольника равны между собой все стороны и углы. Будут ли фигуры, образованные внутренними и внешними контурами, подобны? Почему?

844. 1) Стороны прямоугольника равны а и b (a > b). Середины больших его сторон соединены. Каково должно быть соотношение между а и b, чтобы полученные прямоугольники были подобны данному прямоугольнику?

2) Являются ли стандартные форматки, используемые в черчении, подобными многоугольниками?

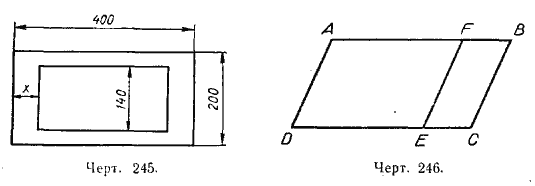
845. На чертеже 245 изображена рамка. Каков должен быть размер х, чтобы внутренний четырёхугольник был подобен внешнему (ширина противоположных планок рамки одинакова)?

846. На чертеже 246 изображён параллелограмм ABCD со сторонами АВ = а и ВС = b, от которого отсечён другой параллелограмм FBCE, подобный данному. Какова должна быть величина отрезка BF?

847. 1) Стороны четырёхугольника равны 14 см, 21 см, 10 см и 42 см. Определить стороны подобного ему четырёхугольника, если известно, что его меньшая сторона равна 2 см.

2) Стороны четырёхугольника относятся, как 1 : ¹/₂: ²/₃: 2, периметр ему подобного четырёхугольника равен 75 см. Найти его стороны.

848. Стороны одного четырёхугольника равны 10 дм, 15 дм, 20 дм и 25 дм, в подобном ему четырёхугольнике сумма наибольшей и наименьшей сторон равна 28 дм. Найти стороны второго четырёхугольника.

849. Наибольшие стороны двух подобных мнбгоугольников равны 35 м и 14 м, а разность их периметров равна 60 м. Найти периметры каждого многоугольника.

Отношение площадей подобных фигур.

850. 1) Стороны квадратов относятся, как 2:3. Как относятся их площади?

2) Стороны равносторонних треугольников равны 6 и 7 см. Чему равно отношение их площадей?

851. На диагонали данного квадрата, как на стороне, построен другой квадрат. Как относятся площади этих квадратов?

852. Площади двух квадратов относятся, как 3 : 5. Чему равна сторона меньшего квадрата, если сторона большего квадрата равна 6 см?

853. 1) Какую часть площади данного треугольника составляет площадь треугольника, отсечённого от него средней линией?

2) В треугольнике проведены все средние линии. Какую часть площади данного треугольника составляет площадь треугольника, образованного средними линиями?

854. Площадь данного многоугольника равна 45 см². Чему равна площадь многоугольника, ему подобного, если сходственные стороны многоугольника равны 10 сми 15 см?

855. Прямая, параллельная стороне треугольника, делит его на две равновеликие части. В каком отношении делит эта прямая другие стороны треугольника?
Чему равен периметр меньшего треугольника, если периметр данного треугольника равен 52 см?

856. План некоторого участка начерчен в масштабе 10 м в 1 см. Во сколько раз площадь участка больше площади плана?

857. На чертеже 247 дан план участка. Определить, проведя необходимые построения и измерения, его площадь. План вычерчен в масштабе 1 : 1000.

858. Построить четырёхугольник, подобный данному, площадь которого была бы больше площади данного многоугольника: а) в 4 раза; б) в 2 раза.

859. Пользуясь поперечным масштабом, измерить отрезки а, bи с, данные на чертеже 224.

860*. Боковая сторона треугольника разделена в отношении 2:3:4 (считая от вершины) и из точек деления проведены прямые, параллельные основанию. В каком отношении разделилась площадь треугольника?

861*. Прямая, параллельная основанию треугольника, делит его боковую сторону в отношении 5 : 3 (считая от вершины), а площадь — на части, разность которых равна 56 см². Определить площадь треугольника.

862*. Треугольник разделён двумя прямыми, параллельными основанию, на три равновеликие части. В каком отношении, считая от вершины, разделились его боковые стороны?

863. Сумма площадей трёх подобных многоугольников равна 232 см², периметры их относятся, как 2:3:4. Определить площадь каждого многоугольника.

864. В прямоугольном треугольнике катеты относятся, как 3 : 4, высота делит площадь треугольника на части, разность которых равна 84 дм². Определить площадь данного треугольника.

ОТВЕТЫ