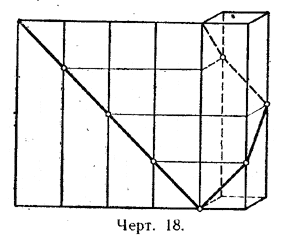
§ 7. Параллелепипеды и призмы.

Диагонали параллелепипеда.

1. Определить диагонали прямоугольного параллелепипеда по трём его измерениям:  1) 1; 2; 2;  2) 2; 3; 6;  3) 6; 6; 7;  4) 8; 9; 12;  5) 12; 16; 21.

2. 1) Боковое ребро прямого параллелепипеда равно 5 м, стороны основания равны 6 м и 8 м и одна из диагоналей основания равна 12 м. Определить диагонали параллелепипеда.

2) В предыдущей задаче заменить данные числа по порядку следующими: 9 см, 7 см,  11 см  и 14 см.

3.   В   прямом   параллелепипеде   стороны   основания   3 см  и 5 см, а одна из диагоналей основания 4 см. Меньшая диагональ  параллелепипеда с плоскостью основания составляет угол в 60°. Определить диагонали параллелепипеда.

4.   В прямом параллелепипеде стороны основания равны 2 см и 5 см;   расстояние   между   меньшими   из   них   4 см;   боковое ребро равно 2√2  см. Определить диагонали параллелепипеда.

5.   Определить диагонали прямого параллелепипеда, у которого каждое ребро равно а, а угол основания равен 60°.

6.   1) В прямом параллелепипеде стороны основания длиной 3 см и 4 см   составляют   угол в 60°,   а   боковое   ребро   есть средняя пропорциональная между сторонами основания.   Определить диагонали этого параллелепипеда.

2) В прямом параллелепипеде рёбра, выходящие из одной вершины, равны 1 м, 2 м и 3 м, причём два меньших образуют угол в 60°. Определить диагонали этого параллелепипеда.

7.   Ребро куба равно а. Определить расстояние от вершины  куба до его диагонали.

8.   Ребро   куба   равно а.   Найти кратчайшее расстояние  от диагонали до непересекающего её ребра.

9. Доказать, что во всяком  параллелепипеде  сумма  квадратов диагоналей равна сумме квадратов всех рёбер.

Сечения  параллелепипеда

10. 1) В прямоугольном параллелепипеде стороны   основания   равны   7 дм  и   24 дм, а высота параллелепипеда равна 8 дм. Определить площадь диагонального сечения.

2) В прямоугольном параллелепипеде боковое ребро равно 5 см, площадь диагонального сечения 205 см² и площадь основания 360 см². Определить стороны основания.

11.    В прямом   параллелепипеде боковое ребро   равно 1 м, стороны основания равны 23 дм и 11 дм, а диагонали основания   относятся   как  2:3.   Определить   площади  диагональных сечений.

12.   В прямом параллелепипеде стороны основания  17 см и 28 см;    одна   из   диагоналей   основания   равна   25 см;   сумма площадей диагональных сечений относится к площади основания, как  16:15. Определить  площади  диагональных   сечений.

13.   В прямом  параллелепипеде с основанием  ABCD  дано: АВ=29 см, AD = 36 см, BD = 25 см и боковое ребро   равно 48 см. Определить площадь сечения AB₁С₁D.

14.   В прямом параллелепипеде острый угол основания содержит α°; одна из сторон основания равна а; сечение, проведённое через эту сторону и противоположное ей ребро, имеет площадь   Q  и   образует   с   плоскостью   основания   угол 90° — α°. Определить другую сторону основания.

15.   Основанием наклонного  параллелепипеда   служит   ромб  ABCD,   в   котором     /  BAD = 60°;   боковые   рёбра   наклонены к плоскости   основания под углом в 60°, и плоскость АА₁С₁С перпендикулярна к плоскости основания. Доказать, что площади сечений BB₁D₁D и АА₁С₁С относятся как 2 : 3.

Призмы.

16.  (Устно.)  Сколько диагоналей можно провести в четырёхугольной призме? в пятиугольной?   в    треугольной?   в   n-угольной?

17.  (Устно.) Сколько плоских углов в пятиугольной призме? сколько двугранных? сколько трёхгранных?

18.  (Устно.)  1) Какие   фигуры   представляют   собой диагональные   сечения   параллелепипеда?   2) Сколько   диагональных сечений можно провести в пятиугольной призме через одно её ребро?  3) На сколько частей эти плоскости (вопрос 2) делят данную призму?   4) Какое тело  представляет   каждая из этих частей (вопросы 2 и 3)?

19.  (Устно.) Сколько диагональных сечений можно провести в n-угольной призме через все её боковые рёбра?

Правильная призма.

20. 1) В правильной четырёхугольной призме площадь основания равна 144 см², a высота равна 14 см. Определить диагональ этой призмы.

2) Определить диагональ правильной четырёхугольной призмы, если диагональ основания равна 8 см, а диагональ боковой грани равна 7 см.

21.  Если в правильной четырёхугольной призме ABCDA₁B₁C₁D₁ диагонали B₁D и D₁B взаимно перпендикулярны, то диагонали А₁С и B₁D образуют угол в 60°. Доказать.

22.  В правильной четырёхугольной призме площадь боковой грани   равна   Q.   Определить площадь диагонального сечения.

23. Основанием призмы служит правильный шестиугольник со стороной а; боковые грани — квадраты.   Определить   диагонали этой призмы и площади её диагональных сечений.

24.  Внутри правильной шестиугольной   призмы,   у   которой боковые грани —квадраты, провести плоскость через сторону  нижнего  основания    и противолежащую   ей   сторону верхнего   основания.   Сторона основания равна а. Определить площадь сечения.

25.   Каждое ребро правильной треугольной призмы а = 3м. Через сторону основания и середину оси проведена плоскость. Найти площадь сечения.

26.  Сторона основания правильной четырёхугольной призмы равна   15; высота равна 20.   Найти кратчайшее расстояние  от стороны   основания   до   непересекающей её диагонали призмы.

27.  Квадрат с проведённой в нём диагональю свёрнут в виде боковой поверхности правильной   четырёхугольной призмы,   и,  таким   образом,   диагональ    квадрата   обратилась   в   ломаную линию   (не   плоскую).   Определить   угол   между   смежными   её отрезками   (черт.  18).

Прямая призма.

28. В прямой треугольной призме через одну из сторон основания проведена плоскость, пересекающая противоположное боковое ребро и отклонённая от плоскости основания на 45°. Площадь основания равна Q. Определить площадь сечения.

29.   В  прямой треугольной призме стороны основания равны 10 см,  17 см и 21  см,   а   высота   призмы  18 см.   Определить площадь сечения, проведённого через боковое ребро и меньшую высоту основания.

30. Основанием прямой призмы служит ромб; диагонали призмы равны 8 см и 5 см; высота 2 см. Найти сторону основания.

Наклонная призма

31.   Боковое   ребро l =15 см  наклонной призмы наклонено к плоскости основания под углом α = 30°. Определить высоту   призмы.

32. В треугольной призме (наклонной) из двугранных углов между боковыми  гранямидва содержат: 20°43'28" и 105°27'32". Чему равен третий угол?

33. В   треугольной  призме   (наклонной) расстояния между боковыми рёбрами 37 см, 13 см и 40 см. Найти расстояние между большей боковой гранью и противолежащим боковым ребром.

ОТВЕТЫ