О РЕШЕНИИ ТРЕУГОЛЬНИКОВ.

X. Косоугольные треугольники.

§ 97. Соотношения между элементами косоугольного треугольника.

Начнем с геометрического соотношения между углами треугольника:

А + В + С = 180°.

Заметим некоторые следствия из него.

а) Так как сумма значений А и В + С равна 180°, то синусы их равны, а косинусы различаются знаками; поэтому
sin (B + C) = sin A;   cos (B+C)= — cos A;   cos A = — cos {В + С).

Точно так же:

tg ( B+ C ) = — tg A.

б) Так как сумма значений и  равна 90°, то сходные функции их соответственно равны (§ 17); например:

sin   = cos  ;   sin  = cos    и т. д.

в) Полезно запомнить еще следующие соотношения между угламя треугольника:

l)  sin A + sin B + sin С = 4 cos • cos  • cos

2)  tg A + tg B+ tg C = tg A • tg B •  tg C;

3)  ctg  + ctg  + ctg  = ctg •  ctg • ctg .

Вывод этих формул предоставляется учащемуся.

§ 98. Лемма. Во всяким треугольнике сторона равна диаметру описанного круга, умноженному на синус противолежащего угла.

Обозначая радиус описанного круга через R, докажем, например, что а = 2R • sin A, где угол А есть острый или тупой.

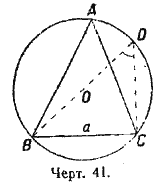
Доказательство. 1) Угол А острый (черт. 41). В oписанном круге из конца данной стороны проведем диаметр и соединим другие концы этой стороны и диаметра; получим прямоугольный треугольник. На чертеже 41 таким треугольником будет BDC; из него, на основании § 21, находим: BC = BD • sin D, или a = 2R• sin D; нo /  D = /  А¹⁾; следовательно, a = 2R• sin A.
¹⁾ Тот и другой измеряются половиной дуги ВС.

2) Угол А тупой. Сделаем такое же вспомогательное построение, как раньше. Из прямоугольного треугольника ВСЕ (черт. 42) найдем: a = 2R• sin E;   но   Е + А = 180°,  следовательно  sin E = sin A, поэтому a = 2R• sin A. Итак, вообще:

a = 2R• sin A;   b = 2R• sin B;    c = 2R• sin C.

§ 99. Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов.

Требуется доказать, что:

^a/_{sin A}  = ^b/_{sin B} = ^c/_{sin C}

Доказательство.   По  § 98 для  всякого треугольника как остроугольного, так и тупоугольного имеем:

a = 2R• sin A;   b = 2R• sin B;    c = 2R• sin C.

Отсюда находим:

2R = ^a/_{sin A} ;  2R = ^b/_{sin B} ;  2R = ^c/_{sin C} ,

следовательно:

^a/_{sin A}  = ^b/_{sin B} = ^c/_{sin C} = 2R.

Таким образом, для одного и того же треугольника частное от деления стороны на синус противолежащего угла есть величина постоянная, равная диаметру описанного круга.

Из соотношения ^a/_{sin A}  = ^b/_{sin B} = ^c/_{sin C} , переставляя члены пропорции, получим:

a : b : c = sin A : sin B : sin С,

т. е. во всяком треугольнике стороны, относятся между собой, как синусы противолежащих углов.

Пример. Определить a : b : c, если А : В : С= 3 : 4 : 5.

Так как А + В + С =180°, то сначала разделим 180° в отношении 3 : 4 : 5; получим
А = 45°, B = 60° и С = 75°. Теперь по доказанному будем иметь:

a : b : c = sin 45° : sin 60° : sin 75°.

Подставляя сюда        _                      _

sin 45° = ^√2/₂,   sin 60° = ^√3/₂   и    sin 75° = cos ^30°/₂=  ¹/₂  

получим, освободясь от знаменателей:

a : b : c = √2   : √3  : .

§ 100. Теорема. Сумма двух сторон треугольника так относится к их разности, как тангенс полусуммы противолежащих углов относится к тангенсу полуразности тех же углов.

Доказательство. По §98 находим:

a + b = 2R {sin A + sin В)  и  а — b = 2R (sin A — sin В);

отсюда:

Применяя здесь ко второй части формулу (XVII) (§ 65), получим:

( a + b ) : (а — b ) = tg  : tg     ,

чем и выражается теорема.

§ 101. Формулы Мольвейде. Так называются следующие две пропорции, которые содержат отношения суммы и разности двух сторон треугольника к третьей стороне:

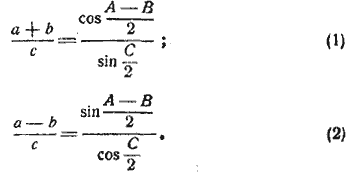
Доказательство. 1) По §98:

a + b = 2R (sin A + sin B)   и   c = 2R • sin C;

отсюда

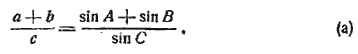
Преобразуем вторую часть:

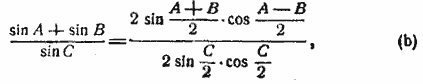
но sin  = cos , так как +  == 90°.  По  сокращении же дроби (b) будет окончательно:

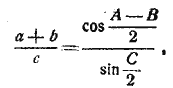
2) Таким же образом получим:

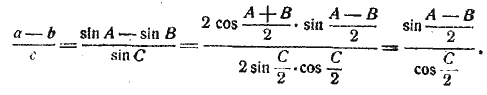
§ 102. Теорема. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения их на косинус угла между ними.

Требуется доказать, что а² = b² + с² — 2bс • соs A (одинаково и в случае острого и в случае тупого;

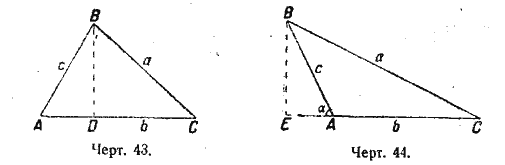
Доказательство. 1) Если угол А острый, то на основании теоремы геометрии о квадрате стороны, лежащей против острого угла, имеем (черт. 43):

а² = b² + с² — 2b • AD,

но из прямоугольного треугольника ABD можно заменить AD через с • cos A; тогда получим:

а² = b² + с² — 2bс • соs A.

2) Если угол A тупой, то применяем теорему о квадрате стороны против тупого угла треугольника (черт. 44). Получаем

а² = b² + с² + 2b • AE.

Из треугольника ABC находим:

AE = с • соs α,

но так как

α = /  BAE = 180° — А,

то

cos α  = cos (180° — А) = — cos A,

поэтому

АЕ = — с • cos A.

Подставляя   это   выражение   в   геометрическую   формулу,   получим:

а² = b² + с² — 2bс • соs A,

т, е. то же самое, что и в первом случае.