О РЕШЕНИИ ТРЕУГОЛЬНИКОВ.
X. Косоугольные треугольники.
§ 106. Выражения для площади треугольника.
Из геометрии мы имеем следующие формулы: - .
S = 1/2 bhb (1)
S = √ p(p — a)(p — b)(p — c); (2)
S= r • p. (3)
Выведем теперь выражения, содержащие углы.
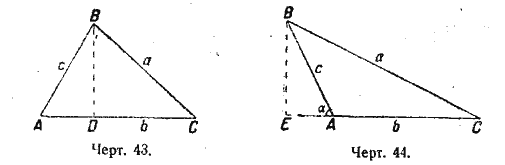
§ 107. а) Возьмем S = 1/2 bhb . Для замены hb обратимся к чертежам 43 и 44:
если угол А острый, то hb = c • sin A;
если угол А тупой, то hb = c • sin α = c • sin (180° — A) = c • sin A.
В обоих случаях имеем hb = c • sin A, т.е. во всяком треугольнике высота равна боковой стороне, умноженной на синус угла между нею и основанием.
Подставляя hb = c • sin A в формулу S = 1/2 bhb, получим:
S = 1/2 bc • sin A (XXV)
т. е. площадь треугольника равна половине произведения двух сторон на синус угла между ними.
б) Из соотношения a/sin A = b/sin B = c/sin C находим:
подставив эти выражения в S = 1/2 bc • sin A , получим:
Так как sin А = sin (В + С), то вместо этой формулы можно взять еще такую:
§ 108. а) Известное из геометрии выражение площади треугольника по трем сторонам нетрудно получить и с помощью тригонометрии.
Мы имеем S = 1/2 bc • sin A , но sin А = 2 sin 
cos , а заменив sin и cos пo §103, получим:
'
б) По § 103 имеем:
Перемножая соответственные части этик равенств, получим по сокращении под корнем:
отсюда:
S = p2 • tg • tg 
• tg 
. (XXVI)
(Между прочим, эта формула полезна в решении треугольников как контрольная.)
§ 109. Выражения для радиуса описанного круга.
1) По § 98 a = 2R • sia A ; отсюда R = a/2sin A.
2) Возьмем R = a/2sin A . Определяя sin А из равенства S = 1/2 bc • sin A,
получим sin A = 2S/bc , а после подстановки: R = abc/4S
§ 110. Выражения для радиуса вписанного круга.
1) Из формулы S= r • p следует: r = S/p.
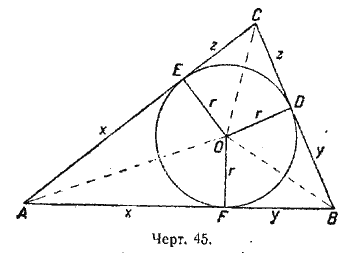
2) По чертежу 45 получим: r = x • tg , но x = р — а; следовательно,
r = (р — а)• tg .
3) Почертегку 45 из /\ /\ BOD и COD имеем: у = r • ctg и z = r • ctg ; складывая и заменяя у + z через а, получим:
